CALENDARS AND CHRONOLOGY
Online Calendar Converters
References and Links
Stern, S. (2012). "Calendars in antiquity :
empires, states, and societies."..
S
Chronology of the Ancient World by Bickerman (1980)
Seidelmann, P. K., et al. (1992). Explanatory Supplement to the Astronomical Almanac, University Science Books.
CHRONOLOGY, ERAS AND CALENDARS
Meeus, 1991 Astronomical Algorithms
Reingold and Dershowitz, Calendrical Calculations: The Ultimate Edition..
RD
Astronomical Calculations: The Julian Day
History of Calendars (Wikipedia)
Grumel, V. (1958). La chronologie, Presses Universitaires de France..
G
GE
Grumel, V. (1934). L Annee du Monde dans la Chronographie de Theophane. Echos d Orient 33: 396 - 408.
Other works by Vernace Grumel
Finegan, J. (1998). Handbook of biblical chronology : principles of time reckoning in the ancient world and
problems of chronology in the Bible. Peabody, Mass., Hendrickson Publishers..
F98
Research Project on Calendars of Late Antiquity and the Middle Ages at University College London (UCL)
Research Project on the Hemerlogia at University College London (UCL)
Meimaris Y. E. Βούγια Π Bougia P. & Κριτικάκου Ε. (1992). Chronological systems in roman-byzantine palestine and
arabia : the evidence of the dated greek inscriptions. Research Centre for Greek and Roman Antiquity National
Hellenic Research Foundation = Κεντρον Ελληνικης και Ρωμαικης Αρχαιοτητος Εθνικον Υδρυμα Ερευνων ; Diffusion de Boccard.
Specific Calendars
The Julian Calendar - timeanddate.com
Julian Calendar at scienceworld.wolfram.com
The Julian Calendar is a solar calendar proposed by Julius Caesar and standardized by Augustus. It was modeled on the ancient Egyptian civil calendar.
A normal Julian year has 365 days while leap years, which occur every 4 years, add an additional day to the month of February. No other intercalations are made.
1 January marks the start of a Julian year. By convention, dates before the
Gregorian Calendar reform of 1582 CE
are reported in the Julian Calendar.
A Julian day begins at midnight.
Byzantine Calendar - wikipedia
A.M. – Anno Mundi. This calendar was used by several of the Byzantine authors including Theophanes and Anastasius Bibliothecarius. The calendar is based on the Julian calendar however the year does not begin on 1 January and the starting day, month, and year of this calendar was a point of contention as it was based on an estimate for the start of "creation" (among other things) as interpreted through the Septuagint - a Greek translation of the Old Testament. An ongoing several hundred year long theological debate over when Biblical "creation" began led to multiple versions of the A.M. calendar. The earlier Byzantine sources used the Alexandrian version (A.M.a) or “Alexandrian era” of this calendar which has a starting date of 25 March 5492 BCE or, according to Bickerman (1980), 25 March 5493 BCE. Earthquake catalogers Guidoboni et al (1994) and Ambraseys (2009) assume a starting date of 25 March 5492 BCE and that is what I use. As explained by Grumel (1958:219)
The Alexandrian era of Panodorus began in 5493 BCE [and] the Alexandrian era of Annianos began in 5492 BCE. The Alexandrian Era of Annianos is what is commonly called the Alexandrian era.Another reckoning system, used for example by Megas Chronographos, is the Byzantine version (A.M.Byz) which has a starting date of 1 September 5509 BCE (Bickerman, 1980:73-74). Yet another reckoning system is a variant suggested in Chronicon Paschale which was composed in ~630 CE. The starting date for this system is 21 March, 5507 BCE. In the Anno Mundi calendar system used by the Byzantine authors, the day followed the Roman civil custom of beginning the calendarical day at midnight. When hours are indicated they mark time since dawn. Hence, if daybreak began at 6 am, the 4th hour would correspond to 10 am (Rautman, 2007:3).
Calendaric Inconsistencies of Individual Authors
| Author | Inconsistencies |
|---|---|
| Theophanes | Grumel (1934:407), Proudfoot (1974:373-374), and others have pointed out that Theophanes A.M.a in the years A.M.a 6102-6206 and A.M.a 6218-6265 are frequently a year too low. |
Indictions - wikipedia
Chart of Indictions
Indictions - An indiction (Latin: indictio, impost) was a periodic reassessment of taxation in the Roman Empire which took place every fifteen years.
In Late Antiquity, this 15-year cycle began to be used to date documents and it continued to be used for this purpose in Medieval Europe. Indictions
refer to an individual year in the 15 year cycle; for example, "the fourth indiction" came to mean the fourth year of the current indiction. Since
the cycles themselves were not numbered, other information is needed to identify the specific year. When an ancient author supplies an indiction along
with an A.M. date, the result may be greater chronological precision. For our dating purposes, indictions began in 312 CE when they were introduced by the Roman Emperor
Constantine. The indiction was first used to date documents unrelated to tax collection in the mid-fourth century.
By the late fourth century it was being used to date documents throughout the Mediterranean.
In 537 CE, Roman Emperor Justinian decreed that all dates must include the indiction.Outside of Egypt, the year of the indiction generally began on 1 September (Bickerman, 1980:78).
Syriac Calendar
Names of months and days in the Syriac Calendar
Automating the Liturgical Calendar of the Syriac Orthodox Church
The Anno Graecorum (A.G.) Calendar is also known as the Seleucid Era, Chaldean, or the
Macedonian Calendar.
This calendar began at the start of the Seleucid Empire and was
assimilated into the Babylonian calendar with Macedonian month-names sometimes substituted for the Babylonian names (Stern, 2012:238). The A.G. calendar uses the same
19 year cycle of intercalations as the Babylonian calendar. There are two start dates. The Macedonian reckoning used
by court officials in the Seleucid Empire and native Greek speakers started in the Autumn of 312 BCE with the start date eventually getting fixed
to 1 Oct. 312 BCE. The Babylonian reckoning used by most Semitic speaking populations has a start date of 1 Nisan in 311 BCE. Ambraseys (2009) equates this
to 1 April, Guidoboni et al (1994) equate this with 2 April, and others equate it to 3 April. A version of the A.G. calendar was used by the Christian Syriac authors such as Pseudo-Dionysius of Tell Mahre
and Chronicon Ad Annum 1234. Syriac writing authors would have likely used the
Macedonian reckoning as this was the standard usage among these authors for the Seleucid era (Sebastian Brock, personal communication, 2021 – see also Stern, 2012:236).
In the Anno Graecorum calendar system, the day starts at sundown (Sebastian Brock, personal communication, 2022).
| Macedonian Month | Julian Equivalent | Duration (days) |
|---|---|---|
| Xanthikos | 22 March - 20 April | 29 |
| Artemisios | 21 April - 20 May | 30 |
| Daisios | 21 May - 19 June | 29 |
| Panemos | 20 June - 19 July | 30 |
| Loos | 20 July - 18 Aug. | 29 |
| Gorpiaios | 19 Aug. - 17 Sept. | 30 |
| Hyperberetaios | 18 Sept. - 17 Oct. | 29 |
| Dios | 18 Oct. - 16 Nov. | 30 |
| Apellaios | 17 Nov. - 16 Dec. | 29 |
| Audynaios | 17 Dec. - 15 Jan. | 30 |
| Peritios | 16 Jan. 14 Febr. | 29 |
| Dystros | 15 Febr. - 16 March | 30 |
| Epagomenai | 17 March - 21 March | 5 |
The Coptic Calendar - Claremont Coptic Encyclopedia
The Coptic Calendar - timeanddate.com
The Coptic Calendar by Bishoy Dawood
Converts from Julian to Coptic and other calendars
Chaine, M. (1925). La chronologie des temps chrétiens de l'Égypte et de l'Éthiopie; historique et exposé du calendrier et du comput de l'Égypte et de
l'Éthiopie depuis les débuts de l'ère chrétienne à nous jours, accompagnés de tables donnant pour chaque année, avec les caractéristiques astronomiques
du comput alexandrin, les années correspondantes des principales ères orientales, suivis d'une concordance des années juliennes, grégoriennes,
coptes et éthiopiennes avec les années musulmanes, et de plusieurs appendices, pour servir à la chronologie. Paris, P. Geuthner.
The Coptic Calendar is also known as the Alexandrian Calendar. The Coptic Calendar is coordinated with the Julian Calendar and, since the 4th century CE, used a
starting year (Year 1) from 29 August 284 CE to 28 August 285 CE. A year consists of 13 months where the first 12 months have 30 days each followed an epagomenal
month which has 5 days during normal years and 6 days during leap years. This version of the Coptic calendar is frequently called the Era of Martyrs and is
frequently abbreviated as A.M. (Anno Martyrum). Coptic Leap Years are coordinated with Julian leap years however the coptic leap day is added on the last day
of the coptic year rather than on 29 February. If a Coptic year will encompass a Julian Leap year (i.e. a year where there will be a February 29),
the coptic year will start on 30 August instead of 29 August as 29 August in the previous Coptic year will be a leap day. In years such as this, the
coptic day will be a day ahead of the Julian Calendar until 29 February. Thus, for example while 21 Tuba normally corresponds to 16 January, in a Julian Leap Year
it will correspond to 17 January. The Coptic day begins at sunrise in the civil calendar and sunset in the liturgical version (Coptic Encyclopedia).
The Islamic Calendar - timeanddate.com
A.H. – Anno Hegirae is also known as the Muslim Calendar or the Islamic lunar calendar. The start date is the Hijra - when on Friday 16 July 622 CE, Mohammed and his followers
migrated from Mecca to Medina. The calendar consists of 12 alternating months of 30 and 29 days. Although the original calendar determined the start of each month based
on astronomical observation of the first visible crescent after a new moon, a fixed tabular calendar was developed in the 8th century CE. In the tabular calendar,
a day is added to the final (12th) month during leap years making it 30 days long instead of 29. Leap days are added every 2-3 years in a 30 year cycle which is
subject to local variation. The most common distribution is on the 2nd, 5th, 7th, 10th, 13th, 16th, 18th, 21st, 24th, 26th, and 29th year of each 30-year cycle (timeanddate.com).
The Islamic day begins at sundown.
Hebrew Calendar Calculator
The Hebrew Calendar - wikipedia
Stern, S. (2001). Calendar and Community: A History of the Jewish Calendar, 2nd Century BCE to 10th Century CE..
S
Seasonal Drift of the Hebrew Calendar
The Hebrew Calendar is also known as the Jewish Calendar or HaLuah HaIvri (הַלּוּחַ הָעִבְרִי) in Hebrew. The Hebrew Calendar is a lunisolar calendar influenced by the Ancient
Babylonian Calendar which has undergone revisions over time. Initially, this calendar was based on sightings of the first crescent after the new moon. After the
destruction of the 2nd temple in 70 CE and throughout the diaspora, the calendar was subject to local variations. By the 4th century CE, a calendar had emerged
which was increasingly based on predicted lunar cycles. Sometime before the 8th century, a fixed 19 year Metonic cycle of intercalations similar to the Babylonian
cycle was adopted and by the early 10th century, the rabbinic calendar had become like the fixed and predictable calendar that is used today. (Stern, 2012:334-335),
The structure of the Hebrew Calendar is one of 12 months with an additional intercalary month added in years 3, 6, 8, 11, 14, 17, and 19 of the
Metonic cycle along with a complicated set of rules (Reingold and Dershowitz, 2018:Section 8.1).
The modern Hebrew Calendar is also characterized by a change in the start date of the calendar from the destruction
of the second Temple in 70 CE to the start of “creation”
like the Anno Mundi Calendar of the Byzantines.
In the Hebrew Calendar, the day begins at sundown.
4.4.1 The Present-Day Rabbinic Calendar: An Outline
- The conjunction (molad) is calculated on the basis of two values
- the mean lunation (duration of the lunar month) of 29 days, 12 hours, and 793 parts (there are 1080 parts to an hour).
- molad of Tishre year 1 (of the era of creation, i.e. the first Tishre in ‘history’), which is given as 2nd day (Monday), 5 hours (of the 24-hour period beginning in the evening), 204 parts, or in its Hebrew acronym: (BaHaRaD). This corresponds to Sunday, 6 October 3761 BCE at 23 hours, 11 minutes, and 20 seconds (assuming the day begins at 18 hours). The molad of Tishre year 1 functions as an epoch (reference point). Any subsequent molad can be worked out by adding the right number of lunations to this epoch. As an alternative to BaHaRaD, the molad of the following Tishre (year 2) can also be used. This molad is 6th day (Friday), 14 hours, no parts (acronym: WeYaD).The fact that this epoch is a round figure (with no parts of the hour) suggests that this was the original epoch to have been in use.
- The month begins, apriori, on the day of the molad. Sometimes it is postponed by one or more days, because of the rules that follow (iii–iv), which are hence known as ‘postponement’ rules.
- Rosh ha-Shanah, 1 Tishre, cannot occur on Sunday, Wednesday, on Friday. This rule is known by its Hebrew mnemonic: (lo ADURosh). If the molad of Tishre occurs on any of these days, the 1st of the month must be postponed.
- If the molad of Tishre occurs on or after the 18th hour (i.e. midday), the 1st of the month must be postponed. (footnote: If the following day is either Sunday, Wednesday, or Friday, Rosh ha-Shanah must be postponed till the day after, hence a postponement of two days.) This is known as molad zaqen (‘late conjunction’).
- The calendar consists of a fixed alternation of 29 and 30 day months: there are always 30 days in Nisan, 29 days in Iyyar, etc. Only the months of Marḥeshwan and Kislew are subject to variation: they can be ‘regular’ (i. e. 29–30), ‘full’ (i.e. 30–30), or ‘defective’ (i.e. 29–29) . This variation makes it possible for rules (iii) and (iv) to be observed, i.e. for the subsequent Rosh ha-Shanah(s) (sometimes more than one year ahead) not to occur on the wrong days. This variation also makes it possible to compensate for the discrepancy between the mean lunation under rule (i)(a) and the average month length of 29½ days resulting from a pure alternation of 29- and 30-day months.
- The intercalation is based on a fixed 19-year cycle, which starts at year 1 (from the creation) and within which the following seven years are intercalated: 3, 6, 8, 11, 14, 17, 19. Intercalation consists of an additional 30-day month, which is inserted before Adar and called ‘first Adar’
Onstott (2015:386-388) notes the following:
B. The Priestly and Civil Calendars
1. Cultic Calendar
Throughout the ancient world, civilizations used two different calendar systems: a cultic calendar for religious festivities and a civil calendar for both the Crown's administration and the agricultural year. Both systems were luni-solar, which means they were based on calculable events common between both the moon and the sun.
...
Israel, like other ancient nations, used the solar system to begin the year and to reckon time. Israel's cultic or priestly calendar closely mirrors the calendar in Mesopotamia but is less similar to the civil calendar in Egypt (as we will see in chap. m). The year began with the spring equinox.142 The first day of the new year began on the first day of the first full month (or new moon) after the equinox, placing the new year between the end of March and the first part of May.143
The Hebrew Scriptures only mention four of the months in Israel's original cultic calendar: Aviv, Ziv, Ethanim, and Bul.144 Aviv was the first month of the year, Ziv the second, Ethanim the seventh, and Bul the eighth.145 These names are quite similar to Canaanite names, from which we infer that Israel and Canaan may have shared the same yearly calendrical system since the seasons were the same for Canaanite territory.146 By the time Ezra worked to update and codify Israel's various manuscripts, the names of Canaan's months had virtually been replaced by Babylonian names. As Andrew Steinmann observes, "During the Babylonian exile the Judeans apparently substituted the Babylonian names for the months into Hebrew. These names are occasionally used in the postexilic books of the Tanakh and are common in later Hebrew" (see Table 9.23).147Table 9.23
Onstott (2015)
2. Civil Calendar
Before the Monarchy, Israel had relied solely on the cultic or priestly calendar established in the Torah. Since only one calendar was in play, it produced the straightforward linear chronology used during the Judges' Era. All this changed under the Monarchy, when Israel asked for a king, the people wanted a government similar to other nations (Deut 7:14; 1 Sam 8:20). One practice of ancient monarchies was to employ a second, "fiscal" or civil year.148 Many synchronisms in Scripture indicate that after Samuel instituted the Monarchy, the nation transitioned to a civil calendar, similar to the civil calendars prevalent in Egypt and Mesopotamia.149 While the priestly-cultic calendar began the new year in the spring with the vernal equinox,150 the Monarchy's civil-agricultural calendar began with the autumnal equinox in the fall in the 7th month of Ethanim (i Kgs 8:2), better known as Tishri.151 The famed loth century calendar excavated at Gezer is an example of the Tishri-based agricul-tural/civil calendar.152 This does not mean that the priestly calendar was abandoned but that a second, administrative system was in use by the end of King Solomon's reign.Footnotes142. Wagenaar, Israelite Festival Calendar, 30-44, 62-78; Steinmann, Abraham to Paul, 15-30; Miano, Shadow Steps, 31-32; Steinmann, Abraham to Paul, 12-30; Finegan, Handbook, 16-17, 25-31; Leo Depuydt, Civil Calendar and Lunar Calendar in Ancient Egypt (Belgium: Peeters, 1997) 15-20, 23, 43, 50-56, 61-63.
143. Finegan, Handbook, 29-33.
144. Aviv—Exod 13:4, 23:15; 34:18; Deut 16:1; Ziv-1 Kgs 6:1, 37; Ethanim—Judg 8:2; and Bul-1 Kgs 6:38. See also Steinmann, Abraham to Paul, 12-16.
145. Finegan, Handbook, 30-33 and Steinmann, Abraham to Paul, 13-16.
146. Steinmann, Abraham to Paul, 15. Nisan—Neh 2:1; Esth 3:7. Sivan—Esth 8:9. Kislev— Neh 1:1. Tebeth—Esth 2:16. Shebat—Zech 1:7. Adar—Ezra 6:15; Esth 3:7,13; 8:12; 9:1, 15, 17, 19.
147. Finegan, Handbook, 21-22, 21, 33; Steinmann, Abraham to Paul, 17-21; Thiele, Mysterious Numbers, 44-50; and Wagenaar, Origin and Transformation, 13-24.
148. Finegan, Handbook, 21, 33-35; Steinmann, Abraham to Paul, 17-21; and Thiele, Mysterious Numbers, 44-50.
149. Finegan, Handbook, 21-22, 21, 33; Steinmann, Abraham to Paul, 17-21; Thiele, Mysterious Numbers, 44-50; and Wagenaar, Origin and Transformation, 13-24.
150. Wagenaar, Origin and Transformation, 13-14; and Finegan, Handbook, 29-31.
151. Finegan, Handbook, 21.
152. Wagenaar, Origin and Transformation, 14-17.
Longman, T., Dillard, R.B. (1994). An Introduction to the Old Testament, Zondervan.
Onstott, J. (2015). YHWH Exists, Vol. 1:
Placing God on Trial: an In depth Look at the Validity and Historicity of the Hebrew Scriptures,
Emmanuel Academic Publishing, Incorporated. Excerpts on Micro and Macro Chronology
Schoors, Antoon. The Kingdoms of Israel and Judah in the Eighth and Seventh Centuries B.C.E..
United States, SBL Press, 2013.
Thiele, E. R. (1983). The Mysterious Numbers of the Hebrew Kings, Academic Books. - bookmarked to the start of Chapter 6 - The Chronology of Judah and Israel (841-723 BC) - can be
borrowed with a free archive.org account
The Mysterious Numbers of the Hebrew Kings - Thiele's chronology (wikipedia)
The Bostran era (also called the era of Bostra, the Arabian era or provincial era) was a calendar era
(year numbering) with an epoch (start date) corresponding to 22 March 106 AD. It was the official era of
the Roman province of Arabia Petraea, introduced to replace dating by regnal years after the Roman
annexation of the Nabataean Kingdom. It is named after the city of Bostra, which became the
headquarters of the Sixth Legion stationed in the province.
Comets & Meteors
Kronk, Gary Cometography A Catalog of Comets Vol. 1-6 - not open access - Cambridge University Press
Kronk, Gary W. (1999) Cometography A Catalog of Comets Vol. 1 Ancient-1799: A Catalog of Comets 1
Cambridge University Press - Anna's Archive
Kronk, G. W. (2013). Meteor Showers: An Annotated Catalog. Netherlands: Springer New York. - Google Books - 54 pages can be previewed
Xu, Z., Pankenier, W., Jiang, Y. (2000). East Asian archaeoastronomy : historical records of astronomical observations of China, Japan and Korea.
Netherlands: Taylor & Francis. - Google Books - 49 pages can be previewed - recommended by Gary Kronk as the best English language catalog of comets
Biot, É. C. (1846). Catalogue des comètes observées en Chine depuis l'an 1230 jusqu'à l'an 1640 de notre ère, faisant suite au catalogue de Ma-touan-lin ...
et extrait du supplément du Wen-hian-thoung-khao, et de la grande Collection des vingt-cinq historiens de la Chine ...
Extrait des “Additions à la Connaissance des Temps” pour 1846. - open access at Google Play
Biot, E. (1846). Catalogue: Des étoiles extraordinaires obsenvées en Chine depuis les temps anciens juqu'à l'an 1203 de notre ère.
Biot, E. (1846). Recherches faites dans les grandes collections des historiens de la Chine
Chambers, Georges F., (1909) The Story of the Comets, Clarendon Press, Oxford, 1909.n - open access at archive.org
Cook, D. (1999). A Survey of Muslim Material on Comets and Meteors. Journal for the History of Astronomy, 30, 131 - 160.
Dall’Olmo, U. (1980). Latin Terminology Relating to Aurorae, Comets, Meteors and Novae.
Journal for the History of Astronomy, 11(1), 10-27.
Grumel, V. (1958). La chronologie, Presses Universitaires de France PAGE 458..
G
GE
Ho Peng, Y. (1962). "Ancient and mediaeval observations of comets and novae in Chinese sources." Vistas in Astronomy 5: 127-225..
HPY
Kennedy, E.S. (1957). Comets in Islamic Astronomy and Astrology. Journal of Near Eastern Studies, 16, 44 - 51.
Marsden, Brian G. and Williams, Gareth V. (2008). 17th edition of the Catalog of Cometary Orbits.
United States: Enslow Publishers.
Pingré, A. G. (1784). Cométographie: ou, Traité historique et théorique des comètes, Imprimerie royale. - open access at Google Play
Williams, J. (1871). Observations of comets, from B.C. 611 to A.D. 1640 : Extracted from the Chinese annals. Translated, with
introductory remarks, and an appendix, comprising the tables necessary for reducing Chinese time to European reckoning
and a Chinese celestial atlas. London - open access at archive.org
Astronomical Coordinates - YouTube video
- from Schmude (2010:1-4)
 Fig. 1.2
Fig. 1.2Steps used in naming a comet. See also Table 1.1
(credit: Richard W. Schmude Jr.).
Schmude (2010)
Table 1.1 lists the time intervals and the corresponding letter sequences mentioned in the second box in Fig. 1.2.
 Table 1.1
Table 1.1Time intervals and letter designations which are used in naming a comet
Schmude (2010)
The last name of the person(s) who discovered the comet may be added to this designation, limited, however, to three last names. For example, Comet Hale-Bopp (C/1995 O1) is named after Alan Hale and Thomas Bopp. The full name is Hale-Bopp C/1995 O1, and its designation is C/1995 O1. If two people who have the same last name discover a comet, such as Gene and Carolyn Shoemaker, it would be given the last name of both individuals (Shoemaker). If several people are involved with a discovery at an observatory, the comet may be named after the observatory instead of the individuals. An example of this is Comet Siding Spring (C/2007 K3). Many comets are named after the all-sky survey which resulted in their discoveries. An example would be Comet LINEAR (C/2008 H1). A few of the all sky surveys include the Lincoln Near Earth Asteroid Research (LINEAR), the Near-Earth Asteroid Tracking Program (NEAT), the Catalina Sky Survey (CSS), the Lulin Sky Survey (Lulin) and the Lowell Observatory Near-Earth Object-Search (LONEOS).
A comet is named after its discoverer (or discoverers) provided that it is not a returning comet or it was not discovered previously as another object, such as an asteroid. In rare cases, a comet is named also after the person who determines its orbit. The English astronomer, Edmund Halley, for example, determined that the comets which appeared in 1456, 1531 and 1607 had orbits which were similar to the comet which appeared in 1682, and he predicted that one 1682 comet would return about 1758. (See Comet Science ©2000 by Jacques Crovisier and Thérèse Encrenaz.) The comet returned in 1759 and, hence, it bears his name – Comet (1P/Halley).
If the same person discovers more than one comet a number would follow the name. For example, E. W. L. Tempel discovered two different Short-period comets, one in 1867 and another in 1873. These comets are named Tempel 1 and Tempel 2, respectively. This rule applies also to comets with the names of two or three co-discoverers. For example, Comet Shoemaker-Levy 9 is the ninth comet discovered by the Shoemaker-Levy team.
Most of the Sungrazing comets are discovered by individuals who analyze images made by the Solar and Heliospheric Observatory (or SOHO) probe. These comets are designated in Fig. 1.2 and are named after the SOHO probe instead of the individual who made the particular discovery. A few Sungrazing comets are also named after the Solar Maximum Mission (or SMM) spacecraft, the SOLWIND spacecraft and the Solar Terrestrial Relations Observatory (or STEREO) spacecraft.
The letter C in Fig. 1.2 may be replaced by a P, D or X depending on the nature of the comet. An explanation follows.
If a comet is found to have a short orbital period, it would be given the P/ designation until it is recovered in a second apparition. At this point, the P/Year designation would be replaced with a number followed immediately by an upper case P; and a slash followed by the name of the person who discovered it. The number here is one more than the number of known periodic comets that have reappeared. For example, Comet Hug-Bell (P/1999 X1) was given the full name 178P/Hug-Bell after it reappeared in 2007. Since 177 periodic comets had been assigned numbers before Hug-Bell reappeared, this comet was given number 178.
If a comet is destroyed, or if it fails to appear after several apparitions, it would be given the designation of D/ followed by the year of its discovery. For example, Comet Shoemaker-Levy 9 has been assigned D/1993 F2 since it was discovered in the second half of March in 1993 and was destroyed when it crashed into Jupiter in 1994.
Comets that are believed to be real but lack sufficient position measurements for an orbital determination are given the designation of X/ followed by the year of discovery and the appropriate letter and number code. For example, Comet X/1896 S1 was first seen on Sept. 21, 1896, by L. Swift at Lowe Observatory in California. Apparently he was the only one to see the comet and was unable to determine enough positions for an orbital determination. Kronk lists 18 comets with the X/ designation that people had seen in the nineteenth century. An unusual situation occurs when a comet’s nucleus splits. In this case, each fragment is given the comet designation followed by A, B, C, etc. For example, the nucleus of comet LINEAR C/2003 S4 split into two parts. Astronomers named the two parts LINEAR C/2003 S4-A and LINEAR C/2003 S4-B. Each part is treated as a separate comet.
Astronomers have discovered many objects which were believed to be minor planets but were later determined to be comets. These objects retain their minor planet designation but are given either a C/ or P/ prefix. For example, astronomers imaged a magnitude 19.3 object on Feb. 18, 2004, and reported it as a minor planet. This object was given the minor planet designation 2004 DZ61. A few weeks later, a different group of astronomers at Mauna Kea in Hawaii imaged this object but found that it had a small coma with a faint tail. This object was reclassified as a comet and was given the designation C/2004 DZ61.
The name of the discoverer of the comet will be used whenever possible for the remainder of this book. For periodic comets the P/number designation is used. For C/ comets, the designation is placed in parentheses. Older designations which include a year and a roman numeral or a year and a lower-case letter will not be used.
- from Schmude (2010:4-6)
 Fig. 1.3
Fig. 1.3A comet’s path can be any one of the four modes shown here
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Comets under the gravitational influence of a single large object like our Sun can move in one of four paths. Each of these is illustrated in Fig. 1.3. Comets which move in a circular orbit maintain a constant Sun distance, the Sun being located in the center of such orbit. Comets which move in an elliptical orbit have a varying Sun distance. Ellipses can have different shapes, ranging from nearly circular to very stretched out. See Fig. 1.4.
 Fig. 1.4
Fig. 1.4The ellipse on the left has an eccentricity of 0.1 and is nearly circular. The one on the right has an eccentricity of 0.65 and is much more squashed
(credit: Richard W. Schmude Jr.)
Schmude (2010)
The eccentricity defines how the ellipse is stretched out. If the eccentricity is low the ellipse would have an almost circular shape, whereas if the eccentricity is high, it would be stretched out. The eccentricity is defined as the distance between the two foci points (F1 and F2) divided by the length of the major axis (line segment A B) in the ellipse. See Fig. 1.5.
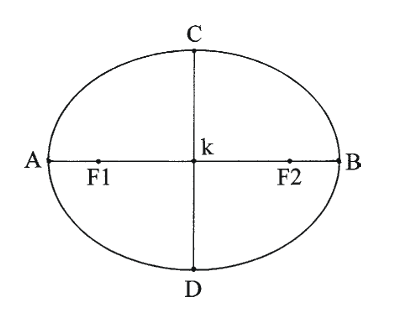 Fig. 1.5
Fig. 1.5The major axis runs from points A to B, and the semi major axis has half the length (A − k or B − k) of the major axis. The two foci points are at F1 and F2. The eccentricity is the distance between the two foci points divided by the length of the major axis. In this example, the eccentricity equals 0.66
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Ellipses can have an eccentricity of just above 0.000 to just below 1.000. Comets which move in circular or elliptical paths will orbit our Sun. Comets which move in a parabolic or hyperbolic path may never return to the Sun. A parabolic orbit has an eccentricity of exactly 1.0. The eccentricity of a hyperbolic orbit is greater than 1.0.
As for orbital elements, which are discussed in the subsection below, one will need to note that all orbital elements have some uncertainty. One source of uncertainty is in the position measurements. Each measurement of a comet’s position has an uncertainty in time, right ascension and declination. A second source of orbital uncertainty is due to gravity. Gravitational forces exerted by other Solar System bodies will change a comet’s orbit and, hence, its orbital elements. A third source of uncertainty results from several types of non-gravitational forces. These non-gravitational forces are described later in this chapter. As a result of these uncertainties, a comet may have a computed orbital eccentricity just over 1.0 but, in reality, it may be just below 1.0.
The elliptical and hyperbolic paths have a range of eccentricities, whereas circular and parabolic paths have eccentricities of exactly zero and one, respectively. In nature, comets will follow paths having eccentricities which will be between either zero and one or above one; but never exactly zero or one. Because of this, it is believed that comets should be broken down into three groups which are Short period, Long-period and No future predictions. Comets in the Short-period group have orbital periods of less than 200 years and will have orbital eccentricities below 1.0. Comets in the Long-period group include both periodic comets with orbital periods over 200 years and comets which are not returning to the inner Solar System. Comets in this group have orbital eccentricities near 1.0 or just over this amount. They will follow either elliptical orbits which are very stretched out or hyperbolic orbits. Comets falling into the third category (No future predictions) are either lost or have been destroyed and are given the designation D/. Table 1.2 gives a breakdown of the percentage of each type of comet.
 Table 1.2
Table 1.2Percentages of comets in different groups, families and sub-groups as of mid-2008, with all of the percentages expressed in terms of the total number of C /, P/ and D/ comets. The writer computed the percentages from data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Can a comet following one path be pushed into another one? Yes! The most common situation occurs when a comet enters our Solar System following an elliptical orbit and makes a close approach to one of the planets. As a result, its path would change to a hyperbolic one, and the comet would leave our Solar System.
Of the almost 1,000 comets listed with a C/ designation in the Catalogue of Cometary Orbits 2008 (17th edition) by Brian G. Marsden and Gareth V. Williams, 23% of them have an eccentricity above 1.000000 and 77% of them have an eccentricity below 1.000000.
- from Schmude (2010:6-8)
- The first quantity is the date and time of perihelion passage. Perihelion is the point on the path where the comet is closest to the Sun. If a comet follows an elliptical orbit, this date and time would be specified for each perihelion passage. The symbol for the date and time of perihelion passage is T.
- The comet-Sun distance at perihelion is the second quantity needed for determination of a comet’s path.
This distance is given in
astronomical units with the
symbol of q. This quantity is the distance between the Sun and point q in
Fig. 1.6.
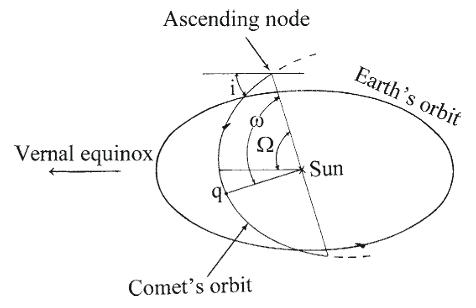 Fig. 1.6
Fig. 1.6
Orbital elements of a comet. The orbital inclination (i), perihelion point (q), longitude of the ascending node (Ω), and argument of perihelion (ω) are illustrated in the drawing. Note that the perihelion distance is the distance between the Sun and point q
(credit: Richard W. Schmude Jr.)
Schmude (2010) - A third quantity is the angle between the plane containing the comet’s path and the plane containing the Earth’s orbit. This angle is called the orbital inclination, and it has the symbol of i. It can range from 0° up to 180°. An inclination of 180° is the same as 0° except that the comet moves in the opposite direction in which the Earth moves around the Sun. If a comet moves in the same direction as the Earth and remains in Earth’s orbital plane, its orbital inclination would equal 0°. The orbital inclination is illustrated in Fig. 1.6.
- A fourth quantity is the comet’s orbital eccentricity. As mentioned earlier, this determines the shape of the path which the comet follows. The symbol for its orbital eccentricity is e.
- The fifth and sixth quantities needed for determination of a comet’s path are the longitude of the ascending node (symbol = Ω) and the argument of perihelion (symbol = ω).
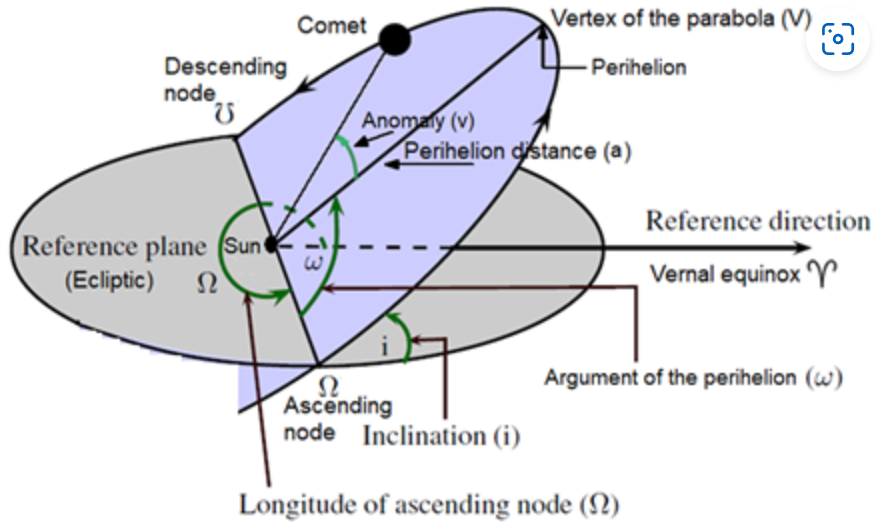 Fig. 6
Fig. 6Comet in a parabolic orbit and associated orbital elements
Bistafa (2021)
- from Britannica
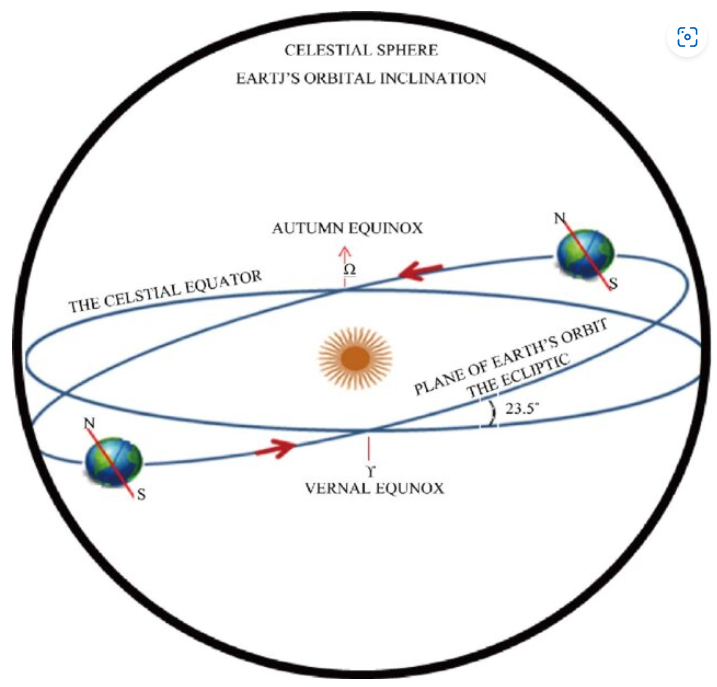 Figure 1
Figure 1Vernal and autumnal equinoxes-Ascending and descending nodes of Earth.
Rama Chandra Murthy Mothe (2014)
CC BY 4.0
- from Schmude (2010:8-9)
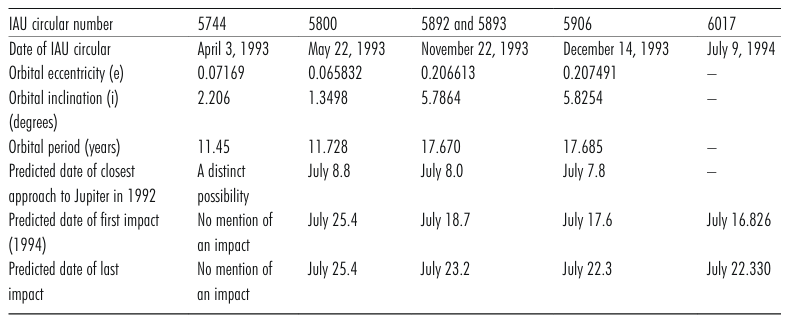 Table 1.3
Table 1.3Orbital elements and other characteristics of Comet Shoemaker-Levy 9 (D/1993 F2) listed in various International Astronomical Union Circulars
Schmude (2010)
- from Schmude (2010:9-10)
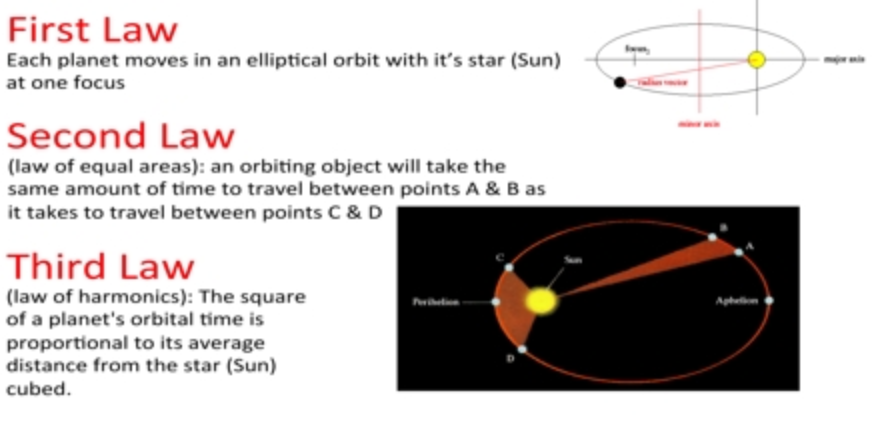 Kepler’s Laws of Planetary Motion
Kepler’s Laws of Planetary MotionJoilet Junior College Astronomy 101 Blog
However, all comets which enter or are in our Solar System experience gravitational tugs by the planets, which are called perturbations. As a result of perturbations, Kepler’s Second and Third laws are compromised, but, in many cases, they may be used as a good approximation of a comet’s movement.
Figure 1.7 shows the orbit of Comet 1P/Halley. Kepler’s Second Law states that a line connecting the Sun to an object that orbits the Sun sweeps out equal areas in equal intervals of time.
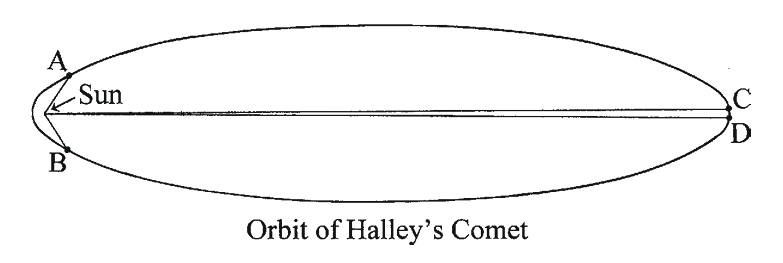 Fig. 1.7
Fig. 1.7A drawing illustrating Kepler’s Second Law of Planetary Motion. It takes Halley’s Comet 1 year to travel from points A to B and from points C to D. Since this comet is close to the Sun at points A and B, it moves much faster than when it is at points C and D. This is due to Kepler’s Second Law which states that a line connecting the Sun to an orbiting planet (or comet) sweeps out equal areas in equal time
(credit: Richard W. Schmude Jr.)
Schmude (2010)
If for example, the area swept out by this line in going from point A to point B equals the area swept out in going from point D to point C then the time it takes for the comet to go from point A to point B will equal the time it takes in going from point D to point C. Obviously the distance between point A and point B is much greater than the distance between point D and point C. Therefore this shows that the comet moves much faster when it is close to the Sun. Figure 1.8 shows approximate velocities of this comet at different points along its elliptical orbit. It moves fastest when it is at perihelion and moves slowest when it is at aphelion – its farthest distance from the Sun. One consequence of Kepler’s Second Law is that a comet moves fastest when it is closest to the Sun (due to stronger gravitational pull).
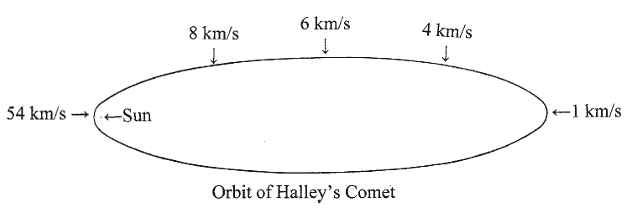 Fig. 1.8
Fig. 1.8A drawing showing the approximate orbital velocities of Comet 1P/Halley at different locations in its orbit
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Comets in an elliptical orbit obey Kepler’s Third Law of Planetary Motion. This law states that for objects orbiting our Sun, there is a relationship between the orbital period and the average distance from the Sun. Essentially, the farther an object is from the Sun, the longer that it will take for that object to orbit the Sun. Kepler’s Third Law in equation form is:
p2 / r3 = 1 year2 / au3 (for objects orbiting our Sun) (1.1)or
r = [p2*au3 / year2] 1/3 (1.2)
In these equations, p is the orbital period, r is the average comet-Sun distance (or the semimajor axis [b in the illustration below] of the comet’s orbit) and au is an abbreviation for astronomical unit. By knowing the orbital period, one can compute the comet’s average distance from the Sun.
 The semi-major (a) and semi-minor axis (b) of an ellipse
The semi-major (a) and semi-minor axis (b) of an ellipseM.W. Toews - Wikipedia - CC0 (public domain)
- from Schmude (2010:10-12)
 Table 1.2
Table 1.2Percentages of comets in different groups, families and sub-groups as of mid-2008, with all of the percentages expressed in terms of the total number of C /, P/ and D/ comets. The writer computed the percentages from data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Long period comets make up 84.7% of all known comets. This group contains two large families of comets – the sungrazer family, with 51.9% of all known comets, and the long-period nearly isotropic family with 32.8% of all known comets. The short-period group contains 13.8% of all known comets, with the Jupiter family making up most of this group.
Comets in a family have similar orbits and are controlled by similar gravitational forces. In many cases, comets in a family also have a similar source. The mathematics used in dividing comets into different families is complex.
Many astronomers rely on the Tisserand Parameter (T) to divide comets into families. According to Encyclopedia of the Solar System, 2nd edition ©2007 by Lucy-Ann McFadden et al., the Tisserand Parameter, T, is defined as
T = (j/r) + 2*[(1-e2)*r/j]1/3*cos(i) (1.3)In this equation j = 5.20280 au and is Jupiter’s average distance from the Sun; r is the comet’s average distance from the Sun; e is the orbital eccentricity of the comet’s path; i is the orbital inclination of the plane containing the comet’s path in degrees; and cos is the cosine function.
The Tisserand Parameter (T) is a useful tool in establishing comet families in the short-period group. Figure 1.9 contains a flowchart illustrating different comet families in this group. If T is less than 2.0, the comet would belong to the nearly isotropic family. If T is between 2.0 and 3.0, the comet would be in the Jupiter family. If T exceeds 3.0, it would be in either the Encke or Chiron family depending on the size of its orbit.
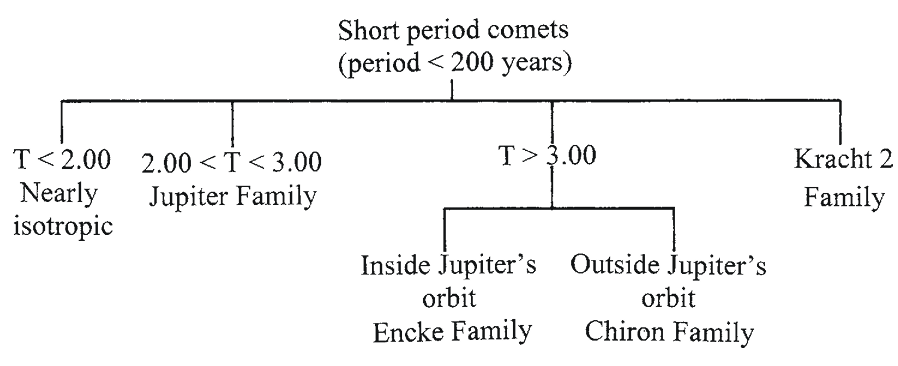 Fig. 1.9
Fig. 1.9A flowchart illustrating the different families of comets within the Short-period group of comets
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Table 1.4 lists several comets, certain orbital elements, Tisserand Parameter values and the families to whom they belong.
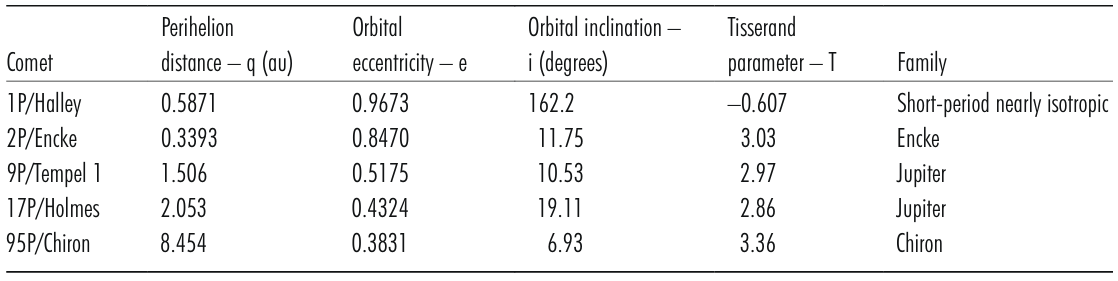 Table 1.4
Table 1.4Orbital elements, the Tisserand parameter (T) and assigned family for a few comets. The general orbital elements of a comet are illustrated in Fig. 1.6; all data in this table are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Figures 1.10–1.12 illustrate the orbits of Jupiter along with the orbits of Comets 2P/Encke, 17P/Holmes and 95P/Chiron, respectively. Comet 2P/Encke lies always inside of Jupiter’s orbit with the Sun, and it never gets close to Jupiter. Comet 95P/ Chiron lies always outside of Jupiter’s orbit, and, hence, it does not get close to Jupiter. Comet 17P/Holmes, on the other hand, may get close to Jupiter, and, hence, Jupiter’s gravity would affect its orbit. In the next section, short-period comets and the families in this group are described.
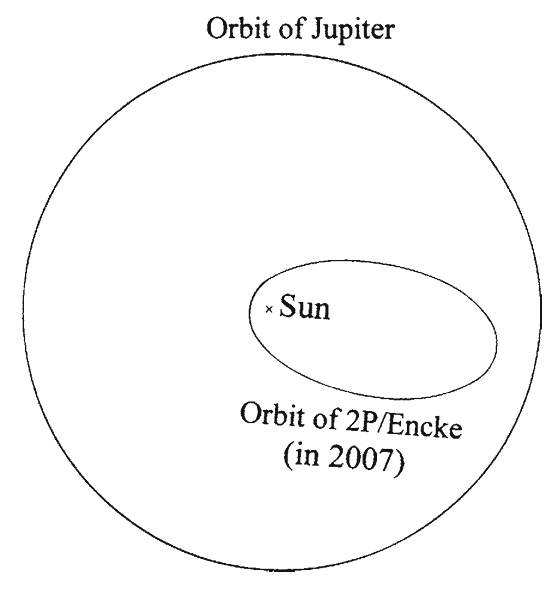
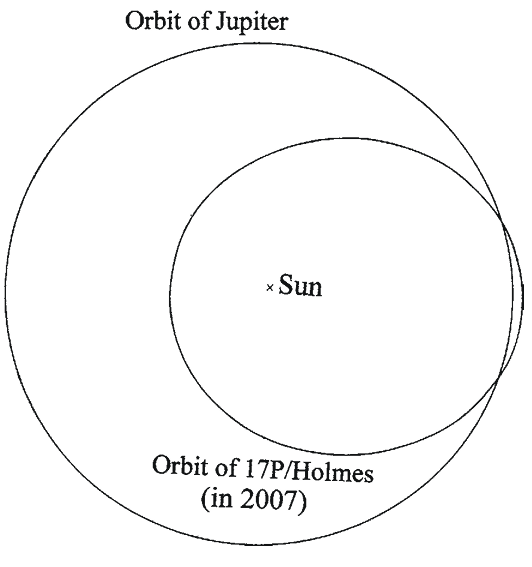
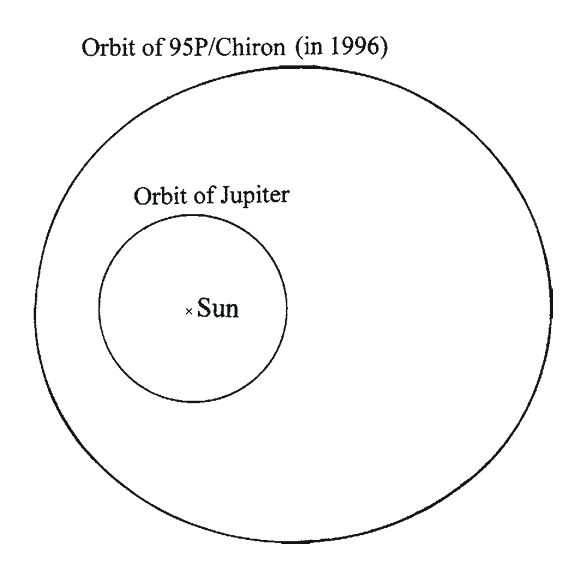 Left
LeftFig. 1.10
A comparison of the orbits of Comet 2P/Encke in 2007 and Jupiter. Note that this comet never gets as far from the Sun as does Jupiter. As a result, it never gets close to Jupiter
Middle
Fig. 1.11
A two-dimensional comparison of the orbits of Comet 17P/Holmes in 2007 and Jupiter. Note that the orbits of the two bodies overlap slightly. This means that they may come closer to one another in time
Right
Fig. 1.12
A comparison of the orbits of Comet 95P/Chiron in 1996 and Jupiter. Note that the comet does not get close to Jupiter
(All credits: Richard W. Schmude Jr.)
All from Schmude (2010)
- from Schmude (2010:12-16)
Comets in the Encke family have orbits inside that of Jupiter. Their movements, however, are not controlled by Jupiter’s gravity. Another of their characteristics is that they have fairly low inclinations. All of them have orbital inclinations below 12°. They, however, may have a wide range of orbital eccentricities, as illustrated in Fig. 1.13. This figure shows a graph of the orbital eccentricity versus the orbital period of comets in the Encke and Chiron families. Therefore, comets in the Encke family follow orbits that range from being nearly circular to those that are stretched out.
Comets in the Chiron family follow paths which lie beyond Jupiter’s orbit. Like the Encke family, these comets are not controlled by Jupiter’s gravity. At least one comet in this family, 95P/Chiron, crosses Saturn’s orbit and, hence, it may make a close pass to that planet. Comets in the Chiron family have low orbital inclinations. All of them have inclinations below 24°, and 63% of them have inclinations below 12°. Comets in this family have a wide range of eccentricities like those in the Encke Family. The orbital periods range from 20 to almost 80 years. See Fig. 1.13.
 Fig. 1.13
Fig. 1.13A graph of the orbital eccentricity versus the orbital period (in years) for comets in the Encke and Chiron Families. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Most of the Short-period comets fall in the Jupiter family. This means that Jupiter’s gravitational field affects strongly their movement. Jupiter family comets can pass close to Jupiter. Jupiter’s orbital inclination is 1.3°, and, hence, most comets in this family have paths that are not in Jupiter’s orbital plane. In spite of this, some of these comets cross Jupiter’s path. Comet Shoemaker-Levy 9 (D/1993 F2) had an orbital inclination of 6.0° but in July 1994, it not only crossed Jupiter’s path but collided with it. Figure 1.14 shows the percentages of Jupiter family comets with different orbital inclinations. Most of these comets have an orbital inclination below 24° which is similar to the Encke and Chiron families.
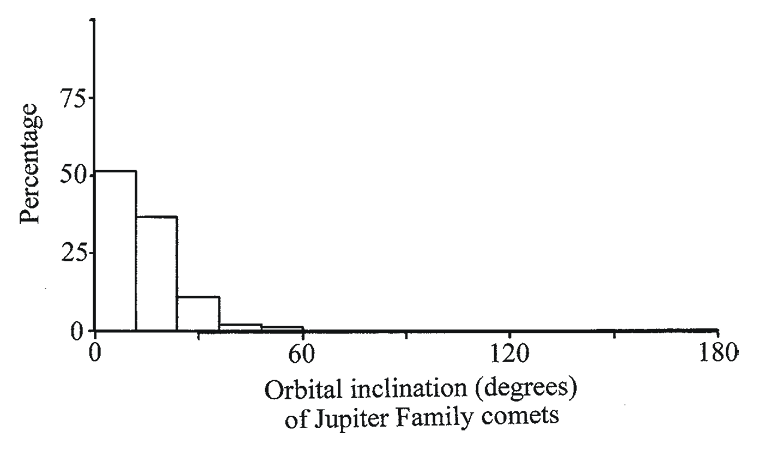 Fig. 1.14
Fig. 1.14A graph of the percentage of comets in the Jupiter Family having different orbital inclinations. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Figure 1.15 shows the orbital period versus orbital eccentricity for Jupiter family comets. Jupiter family comets have a wide range of orbital eccentricities. Those with periods longer than about 25 years tend to have high eccentricities. High eccentricities are the only way that these comets can get close to Jupiter and, hence, come under its gravitational influence.
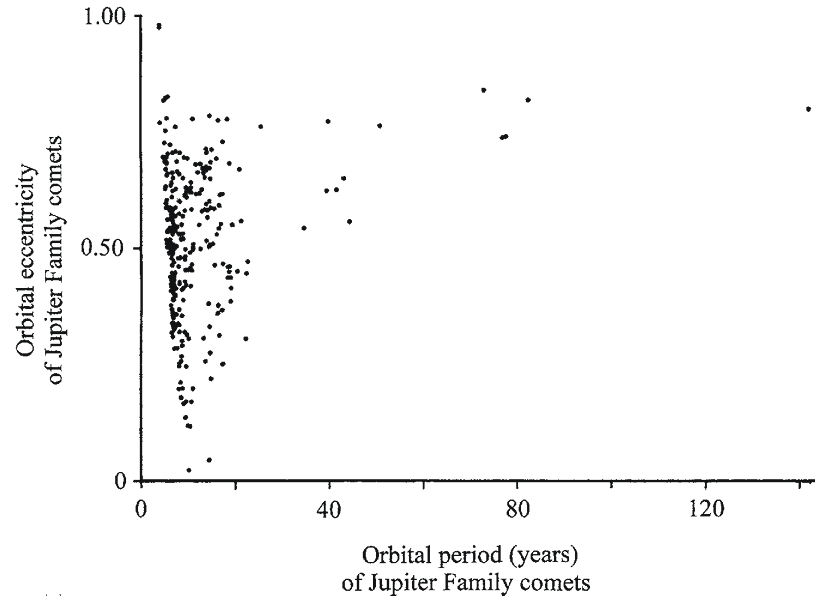 Fig. 1.15
Fig. 1.15A graph of the orbital eccentricity versus the orbital period for comets in the Jupiter family. Note that comets having an orbital period of less than about 15 years have a wide range of orbital eccentricities whereas those with an orbital period above 30 years have orbital eccentricities above 0.5. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Comets in the short-period, nearly isotropic (NI) family have a different distribution of orbital inclinations than those in the Encke, Chiron and Jupiter families. Figure 1.16 shows the percentage of Short-period NI comets with different orbital inclinations. The figure shows that there is a fairly even distribution of orbital inclinations which is in contrast to comets in the Encke, Chiron and Jupiter families.
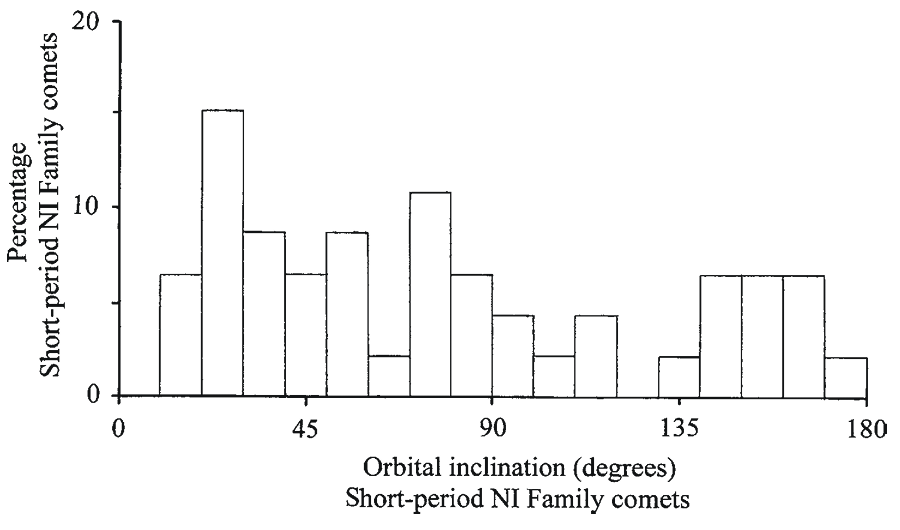 Fig. 1.16
Fig. 1.16This graph shows the percentage of comets in the Short-period nearly isotropic (NI) family with different orbital inclinations. Note the fairly even distribution of orbital inclinations. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
The difference in inclination suggests that there is a different source for the Short-period NI comets compared to the other three families of comets discussed above. Astronomers believe that the Oort Cloud is the main source of short period NI comets because of the almost even distribution of orbital inclinations. The Oort Cloud, named after Dutch astronomer Jan Hendrix Oort, is a spherical shell extending from 3,000 au (or 0.05 light years) to about 100,000 au (or about 1.6 light years) from the Sun. There may be as many as 1012 icy objects in this cloud that are big enough to become comets. Because of the abundance of low orbital inclinations for the Encke, Chiron and Jupiter families, astronomers believe that their main source of origin is the region just beyond Neptune.
Figure 1.17 shows a graph of the orbital eccentricity plotted against the orbital period of Short-period NI comets. (Comets 153P [period = 364 years, eccentric ity = 0.990062] and C/1937 D1 [period = 187 years, eccentricity = 0.981] are not included in Fig. 1.17.) In all cases, these comets have orbital eccentricity values greater than 0.60. This means that comets in this family follow stretched out orbits. They will get close to the Sun for a short period of time and will remain far from the Sun for the remainder of the time.
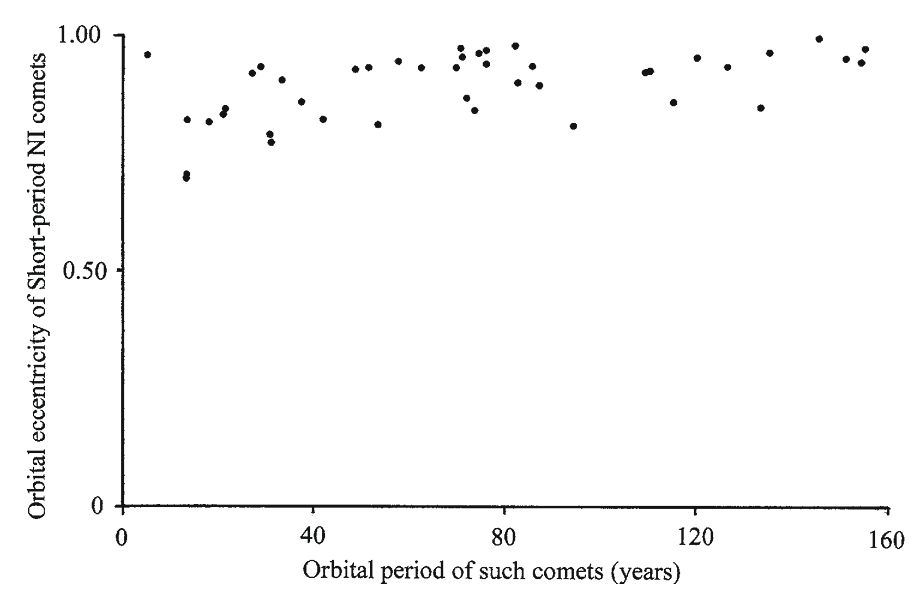 Fig. 1.17
Fig. 1.17A graph showing the orbital eccentricity for different orbital periods of comets in the Short-period nearly isotropic (NI) family with different orbital periods. Note that all of the comets have orbital eccentricities above 0.6. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Finally the Kracht 2 family of comets consists of four members as of mid-2008. These comets may get very close to the Sun. They have an average perihelion distance of 0.054 au. Three of the four Kracht 2 comets have eccentricities of between 0.977 and 0.979, which is consistent with a semimajor axis of about 2.5 au. These comets may get close to Jupiter at aphelion and if so, their orbits may get changed by it. Average values of other orbital characteristics for the Kracht 2 family are listed in the bottom row of Table 1.5.
 Table 1.5
Table 1.5Average orbital characteristics of seven different sub-groups of Sungrazer Family of Long-period comets and one sub-group of Kracht 2 Short-period comets. In some cases, the standard deviation is given in parentheses. All values are based on data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
- from Schmude (2010:16-21)
 Table 1.2
Table 1.2Percentages of comets in different groups, families and sub-groups as of mid-2008, with all of the percentages expressed in terms of the total number of C /, P/ and D/ comets. The writer computed the percentages from data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Figure 1.18 shows a flowchart illustrating different comet families and sub-groups in the long-period group.
 Fig. 1.18
Fig. 1.18A flowchart illustrating the different families of comets and their sub-groups within the Long-period group of comets
(credit: Richard W. Schmude Jr.)
Schmude (2010)
The sungrazers are comets that move in stretched-out orbits and approach the Sun at distances of usually less than 0.05 au. (An astronomical unit is the average Earth-Sun distance and it equals 149.6 million kilometers.) Figure 1.19 shows the orbit of a typical Kreutz family comet – Comet C/2007 V13. The orbit is very stretched out because of the high orbital eccentricity (~0.9999). Essentially this comet is just 0.0057 au from the Sun’s center, or just 157,000 km above the Sun’s photosphere at perihelion. At its farthest point, it is over 172 au from the Sun (assuming an orbital period of 800 years).
 Fig. 1.19
Fig. 1.19The approximate path that Comet C/2007 V13 follows. Note that this path is very stretched out. This comet spends almost all of its time far from the Sun
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Figure 1.20 shows a close-up view of the path of Comet C/2007 V13 as it approached the Sun in 2007. The comet’s path is the dashed curve.
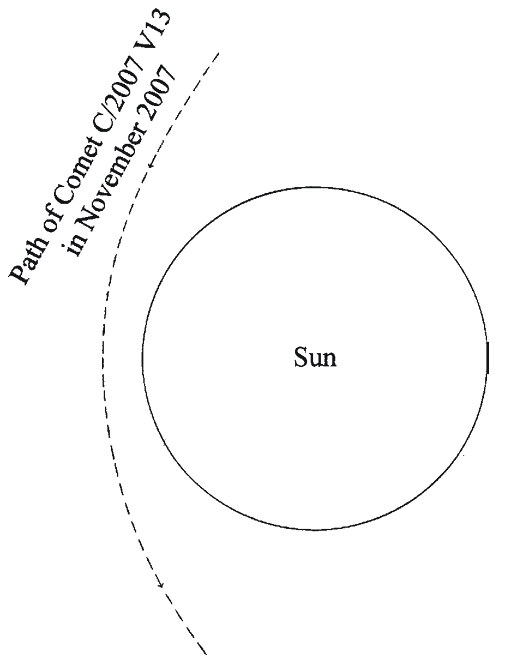 Fig. 1.20
Fig. 1.20The path that Comet C/2007 V13 followed as it made its close approach to the Sun in November of 2007
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Do sungrazing comets burn up when they pass close to the Sun? Oftentimes they do. Many burn up because of their small sizes. Astronomers believe that their nuclei are between a few meters to a few tens of meters across. Others collide with the Sun. At least 26 Kreutz group comets had perihelion distances of less than the radius of the Sun (as of mid-2008), and, hence, they collided with the Sun. Many more sungrazers make such a close approach that they either spiral into the Sun or perhaps sublime or explode during their close pass to the Sun. Some Sungrazers, however, survive their close passage of the Sun. How can this be? This may be answered with a question: Have you ever moved your finger quickly through a candle flame? If you have, it probably did not hurt. This is because you did not allow enough time for your finger to heat up. Many sungrazers also pass by the Sun fast enough to remain intact. These comets move quickly when near the Sun because of Kepler’s Second Law of Planetary Motion. In Fig. 1.20, it took Comet C/2007 V13 about 1.5 h to move from one end of the dashed curve to the other end. Therefore, even though sungrazers get very close to the Sun, they do not get as hot as one might expect.
Figures 1.21 and 1.22 show the distribution of perihelion distances for the Meyer and Kreutz sub-groups, respectively. Comets in the Kreutz sub-group have a narrow range of perihelion distances. Most of these comets pass within 0.01 au of the Sun’s photosphere.
 Fig. 1.22
Fig. 1.22This graph shows the distribution of perihelion distances for the Kreutz sub-group of comets. Note that there is a narrow range of perihelion distances for these comets. Several of these comets crashed into the Sun. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Comets in the Meyer sub-group do not get as close to the Sun. Most of these comets pass within 0.04 au of the Sun’s photosphere.
 Fig. 1.21
Fig. 1.21This graph shows the distribution of perihelion distances for the Meyer sub-group of comets. Note that there is a fairly narrow range of perihelion distances for these comets. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Figure 1.23 shows the distribution of orbital inclinations of a few larger sub-groups of sungrazing comets.
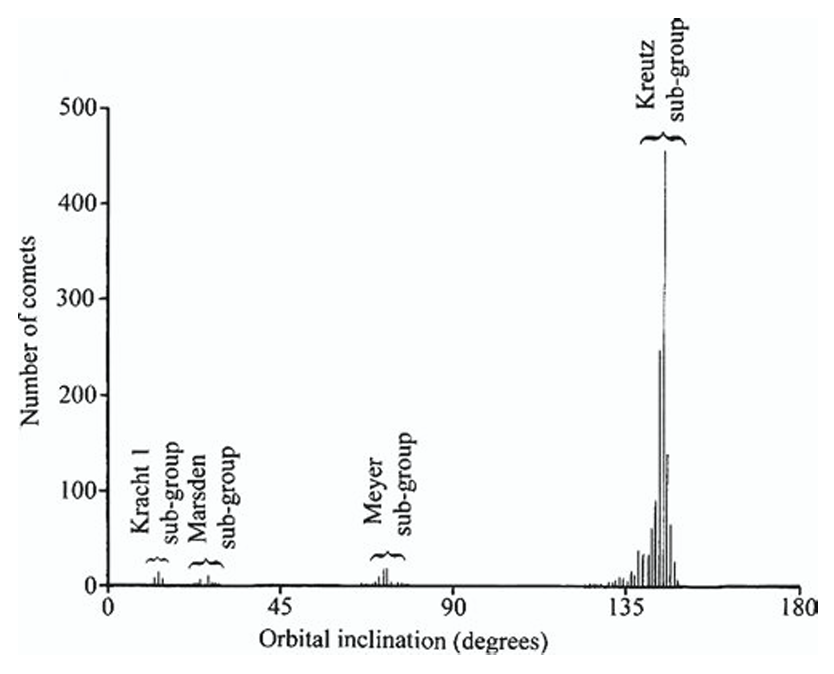 Fig. 1.23
Fig. 1.23This graph shows the distribution of orbital inclinations for different sub-groups of Sungrazing comets. Note that each sub-group has a narrow range of orbital inclinations. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
All of the sub-groups have a narrow distribution of orbital inclinations. This is evidence that the different sub-groups have different sources. Table 1.5 summarizes average values of three orbital quantities in degrees (Argument of perihelion – ω, Longitude of the ascending node – Ω and the Orbital inclination – i) for comets in several sub-groups of the sungrazer family.
 Table 1.5
Table 1.5Average orbital characteristics of seven different sub-groups of Sungrazer Family of Long-period comets and one sub-group of Kracht 2 Short-period comets. In some cases, the standard deviation is given in parentheses. All values are based on data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Comets in the Kreutz sub-group are believed to be fragments of a single comet. Comets in each of the other sub-groups may be fragments of different comets which broke up some time in the past.
I have analyzed the brightness of the sungrazing comet SOHO (C/2001 C5), based on brightness values reported in the International Astronomical Union Circular Number 7585. The brightness values of it are plotted in Fig. 1.24 on different decimal dates in February 2001.
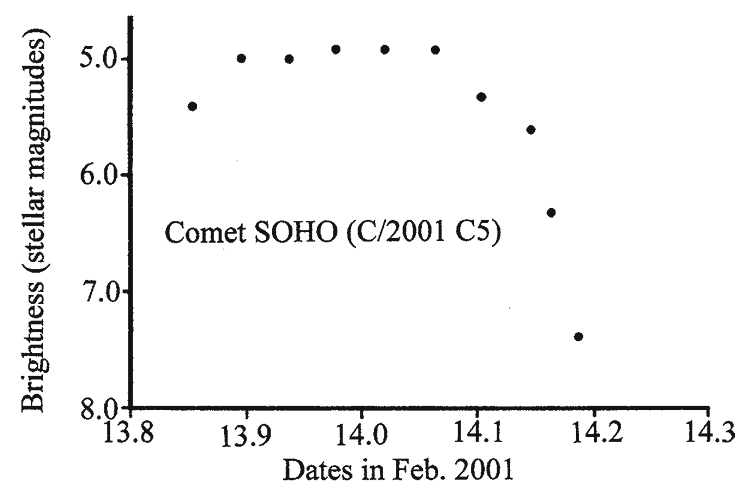 Fig. 1.24
Fig. 1.24This graph shows the brightness of the Sungrazing Comet (C/2001 C5) in stellar magnitudes on different decimal dates in February, 2001. Data are from IAU Circular Number 7585
(credit: Richard W. Schmude Jr.)
Schmude (2010)
The decimal date is the date followed by the fraction of the day that has elapsed since the start of the day (0:00 Universal Time). This comet has a normalized magnitude of H10 = 24.58 (normalized magnitudes are described later in this chapter). This value is almost 18 stellar magnitudes fainter than the average H10 value of comets with a C/ designation. This means that comet SOHO (C/2001 C5) would be just over 10 million times fainter than a typical comet with a C/ designation at the same distance from the Earth and Sun. The only reason why comet SOHO (C/2001 C5) reached a stellar magnitude of 4.9 is because of its close distance to the Sun at the time the measurements were made.
The long-period nearly isotropic (NI) family of comets has a wide range of orbital inclinations. This is similar to the short-period NI comets. The percent ages of orbital inclinations for all NI comets are plotted in Fig. 1.25. The orbital inclinations are fairly evenly distributed between 40° and 150°. The numbers drop off at orbital inclinations of less than 40° and above 160°.
 Fig. 1.25
Fig. 1.25This graph shows the percentage of Long-period and Short-period nearly isotropic (NI) comets having different orbital inclina tions. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
As of mid-2008, 50 sungrazer comets do not belong to any of the seven sub groups of the sungrazer family listed in Table 1.5.
 Table 1.5
Table 1.5Average orbital characteristics of seven different sub-groups of Sungrazer Family of Long-period comets and one sub-group of Kracht 2 Short-period comets. In some cases, the standard deviation is given in parentheses. All values are based on data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
These comets fall into the unclassified (sungrazer) category in Table 1.2.
 Table 1.2
Table 1.2Percentages of comets in different groups, families and sub-groups as of mid-2008, with all of the percentages expressed in terms of the total number of C /, P/ and D/ comets. The writer computed the percentages from data in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
I plotted the orbital inclination versus the argument of perihelion for these comets. After a close study of this plot, along with the longitude of the ascending node values, I concluded, based on the data collected up to mid-2008, that there are no new families for the unclassified comets. Two of these unclassified comets – SOHO (C/1999 O4) and SOHO (C/2004 Y10) – have respective orbital values of (ω = 104.04°, Ω = 107.87°, i = 133.32°) and (ω = 99.02°, Ω = 129.68°, i = 131.61°). Of all of the unclassified Sungrazers, these two have the closest orbital constants. Because of their large difference in the Ω value, it is doubtful that they represent a new family of comets.
- from Schmude (2010:21)
- from Schmude (2010:21-22)
The first object discovered beyond the orbit of the planet Neptune was the newly-classified dwarf planet Pluto. Since the early 1990s, astronomers have discovered over 1,200 objects beyond Neptune’s orbit; and there may be numerous other objects with diameters exceeding a few dozen km between 30 and 50 au from the Sun. These bodies usually have low orbital inclinations and are believed to be a source of short-period comets. A second source of comets is believed to be the Oort Cloud described above. Unlike the objects lying just beyond Neptune, those in the Oort Cloud have a nearly random distribution of orbital inclinations. See Fig. 1.26. These objects cannot become comets as defined, until they pass close to the Sun because, without the Sun’s warmth, they will not develop comas.
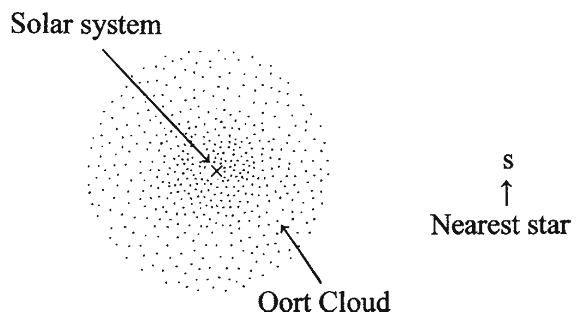 Fig. 1.26
Fig. 1.26This drawing shows the Oort cloud, and the distance to the nearest star (point s) outside of our Solar System (point ×)
(credit: Richard W. Schmude Jr.)
Schmude (2010)
An icy body in the trans-Neptune area (30–50 au from the Sun) may be pulled inwards by Neptune’s gravity. Objects in the more distant Oort Cloud may be pulled inward by gravitational forces exerted by stars passing close to the Sun or by galactic perturbations. When an icy body is pushed inward (and into warmth) it may develop a coma and, hence, become a comet. Forces which may push or pull an icy body towards the Sun are gravity from the Sun, gravity from planets, gravity from nearby stars, and gravity from the galactic disk. These forces will be discussed after a brief discussion of Newton’s Law of Universal Gravitation
- from Schmude (2010:22)
Fg = (G × m1*m2)/D2where G is the gravitational constant, 6.67 × 10-11 m3/(kg s2), m1 is the mass of the first object (let’s say the comet), m2 is the mass of the second object which can be the Sun or a planet, and D is the distance between the centers of m1 and m2. The important trend to note is that the force of gravity (Fg) changes with the square of the distance. Therefore, at small distances, Fg gets large quickly whereas for large distances, Fg gets small quickly. In short, an object’s gravitational force depends on both its mass and distance to a second object.
Although the Sun is the most massive object in our solar system, its gravity may not always exceed that of a nearby planet. Another consequence of Newton’s Law of Universal Gravitation is that the Sun’s gravity grows weaker outside of our solar system. This is because gravity drops off with the square of the distance. For example, the Sun’s gravity is 900 times stronger at a distance of 1.0 au compared to a distance of 30.0 au.
- from Schmude (2010:23-25)
The Sun is the most massive object in our solar system. As a result, comets are drawn towards it. Once an icy object passes into our solar system, it will most likely be drawn towards the Sun. If the conditions are right, it will orbit close to the Sun, develop a coma and become a comet.
Planets can exert a strong gravitational force on a nearby comet and, in many cases, can change the orbital period or direction of a comet. Figure 1.27 illustrates a comet making a close pass to Jupiter.
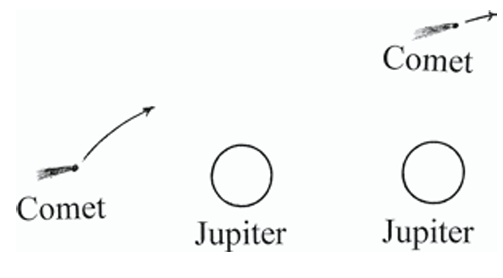 Fig. 1.27
Fig. 1.27As a comet approaches Jupiter, its orbital speed increases as a result of the pull effect of Jupiter’s gravity. This is illustrated with a long, curved arrow. As a comet moves away from Jupiter its orbital speed decreases because of the pull of Jupiter’s gravity against the outward movement from Jupiter. This is illustrated with a short, curved arrow
(credit: Richard W. Schmude Jr.)
Schmude (2010)
As the comet approaches Jupiter, it speeds up (represented by a long arrow) and, as it moves away, it slows down (represented by a short arrow). The comet speeds up as it approaches Jupiter because Jupiter’s gravity is pulling the comet towards it. As the comet moves away, Jupiter’s gravity pulls it back causing it to slow down. Since Jupiter is also moving, operation of the gravitational forces becomes complicated.
It is, however, possible to compute the trajectory of the comet as a result of its close pass to a planet. In most cases, a nearby planet will change both the direction in which a comet moves and its speed. In Fig. 1.27, Jupiter’s gravitational force causes a change in comet speed. Since Jupiter has such a large mass, the gravitational force of a comet has little effect on Jupiter’s movement. The net result of these gravitational forces causes orbital change of the comet.
Each of the planets can change a comet’s orbit. Figure 1.28 shows how the orbital period of Comet 1P/Halley has changed since 239 BC.
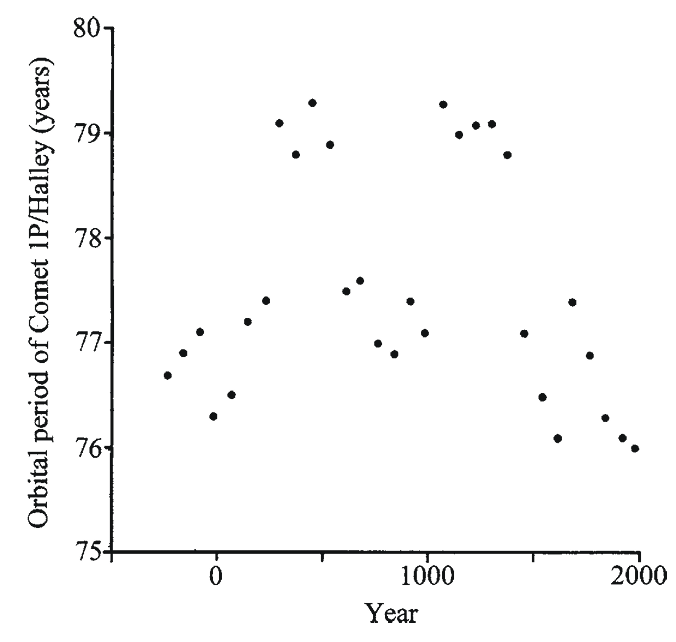 Fig. 1.28
Fig. 1.28This graph shows the orbital period of Comet 1P/Halley since 239 BC. Note that the orbital period has changed over the last 2000-plus years. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit: Richard W. Schmude Jr.)
Schmude (2010)
The period was as high as 79.3 years in 451 and 1066 AD and was as low as 76.0 years in 1986. Much of the change in the orbital period is due to small planetary perturbations. For several periodic comets, Table 1.6 lists the range of their orbital periods, their average orbital periods and the related time intervals. In many cases, a planetary perturbation can cause a comet to change course and head to the inner solar system. Neptune plays an important role for trans-Neptune objects. In a similar manner, a planetary perturbation can eject a comet from our solar system.
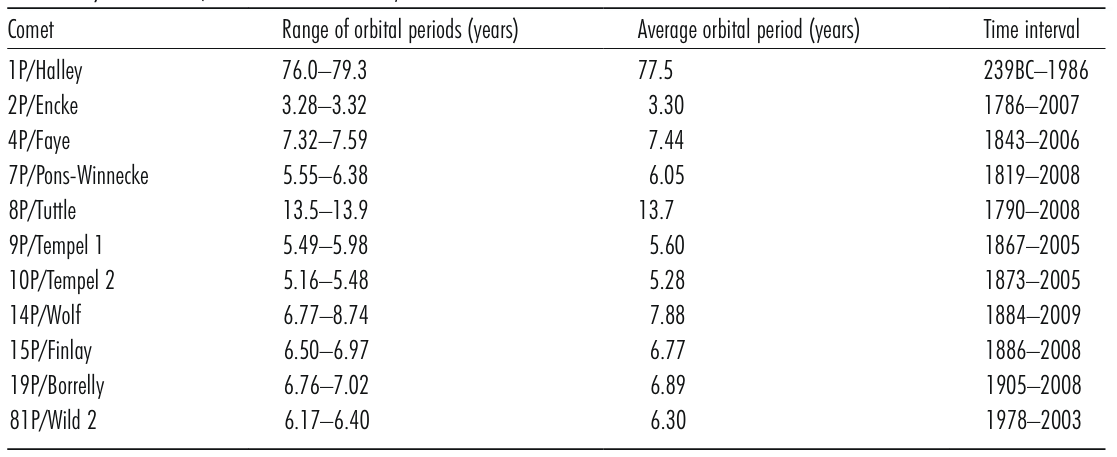 Table 1.6
Table 1.6The range of orbital periods and average orbital periods for several Short-period comets. Data are based on values in Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Schmude (2010)
Our galaxy can also exert a gravitational force on potential comets. Our solar system moves once around the galaxy every 220 million years or so. In addition, our solar system moves through the galactic plane where there is a higher density of matter. The extra mass can exert small gravitational tugs on icy objects in the Oort Cloud. In many cases, objects may be directed to the inner solar system and become comets. One astronomer reported that a group of 152 long-period comets do not have random orbits. This person suggested that gravitational tugs from the galactic disc were responsible for the non-random distribution. (See Astronomy and Astrophysics, Vol. 187, pp. 913–918 by A. H. Delsemme for more information.)
Nearby stars can also nudge objects in the Oort Cloud towards the inner solar system. One group of astronomers reported that about 12 stars pass within 1.0 par sec (or 3.26 light years) of the Sun every million years. Stars passing this close should exert gravitational tugs on some of them in the Oort Cloud causing a few of them to enter and pass through the inner solar system and become comets.
To sum up, a comet may be pushed or drawn into the inner solar system by the Sun, planets, nearby stars, or our galaxy; and the Sun and planets may continue to modify a comet’s path inside of our solar system. Once a comet is in the inner solar system, non-gravitational forces can also play a role in the path that it takes. These forces include those caused by volatile substances escaping from the comet’s nucleus, meteor impacts, the Yarkovsky Effect, sunlight, the solar wind, occasional solar explosions and occasional solar storms. These non-gravitational forces are discussed below.
- from Schmude (2010:25-26)
When an icy body approaches the Sun, its surface warms up and volatiles escape from its nucleus. When this occurs, the nucleus recoils slightly in the opposite direction. I call this the “rocket force”, because a rocket works on the same principle. This recoil is due to Newton’s Third Law of Gravitation which states that for every action, there is an equal and opposite reaction. See Fig. 1.29. The magnitude of the rocket force depends on several factors, including the amount of material leaving the nucleus, the comet’s distance from Sun, orientation of spin axis of the nucleus and the rotation rate of the nucleus.
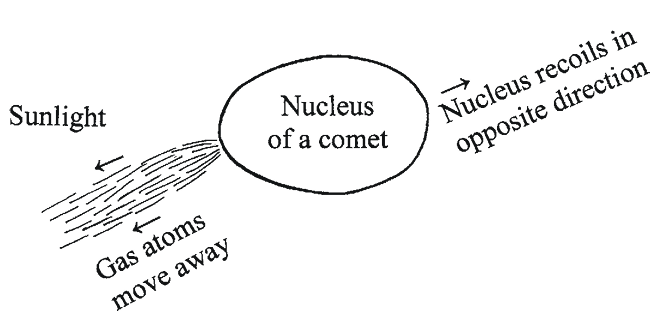 Fig. 1.29
Fig. 1.29As gas escapes from the nucleus, it moves in one direction. Due to Newton’s Third Law of motion, the nucleus recoils slightly in the opposite direction. This movement is one example of a non-gravitational force. Note that sunlight is coming from the left side
(credit: Richard W. Schmude Jr.)
Schmude (2010)
Impacts are a second source of non-gravitational force. During an impact, the impacting body exchanges momentum with the cometary nucleus, causing it to move a little in the direction of the momentum. An object’s momentum is the product of its mass and velocity. The larger the mass or velocity of an object, the greater will be its momentum. Impacting objects may also expose buried ices. These ices will then sublime when the comet approaches the Sun. This, in turn, may lead to an additional “rocket force.” Impacting objects may affect also the rotation rate of the nucleus.
A third type of non-gravitational force results from the non-random reflection of sunlight for a comet. The Yarkovsky Effect is the result of a spinning comet absorbing sunlight and then re-radiating it in a different direction. This non random reflection of sunlight may lead to small pushes in the direction away from where the radiation is released, provided that the nucleus rotates around a single axis. One group reports that this effect shifted the position of the minor planet Golevka 15 km between 1991 and 2003. Comets with small orbits which rotate around a single axis will be most susceptible to the Yarkovsky Effect because a comet in a small orbit receives more sunlight. Furthermore, the Yarkovsky Effect builds up quicker for a nucleus which rotates around a fixed axis compared to one that does not do so.
Sunlight also exerts a small push. This is called solar radiation pressure. Solar radiation pressure pushes in the opposite direction as the Sun’s gravity. Essentially, light possesses momentum which may alter a comet’s momentum. Solar radiation pressure is small compared to the gravitational force of the Sun. Nevertheless, this pressure over many centuries may affect a comet’s movement.
A fifth source of non-gravitational force is exerted by the solar wind. The solar wind consists of protons and other particles leaving the Sun, including gamma rays and X-rays. It generally moves rapidly from the Sun and, hence, exerts a force in a direction opposite to the Sun’s gravity. While solar wind exerts a small force on a comet, over long periods of time, it may result in changes in a comet’s movement or orbit.
In the Catalogue of Cometary Orbits 2008, these non-gravitational forces are lumped together into two parameters, A1 and A2. The radial component is described by A1 and the transverse component is described by A2. The values of A1 and A2 can change over time. For example, the values of A1 and A2 for Comet 2P/Encke were −0.03 and −0.0030 in 1977 but were −0.01 and −0.0007 in 2007. Finally, but not least, the random occurrences of solar explosions and solar storms cannot be overlooked. These phenomena exert slight forces which could affect over time the orbit of a comet within their ranges.
It is very difficult to analyze precisely a comet’s movement and orbit. This is because cometary orbits are not only chaotic, but because they may be affected by so many varying forces – gravitational and non-gravitational – which affect their movement and orbit. Even small forces caused by the “rocket force”, impacts, the Yarkovsky Effect, solar radiation pressure and solar wind pressure may be of importance
- from Schmude (2010:26-28)
Figure 1.30 [left] shows the distribution of orbital inclinations of short-period comets (excluding those with a D/ designation). Most of these comets have orbital inclinations of less than 30° due to the large number of Jupiter family comets in this group. The low inclination of these comets suggests that most of them came from the zone of icy objects just beyond Neptune where orbital inclinations are usually low.
Figure 1.31 [right], plots the distribution of orbital inclinations for all comets known as of mid-2008 except those named SMM, SOHO, SOLWIND, STEREO and those that have been given a D/ designation. There is a fairly even distribution of orbital inclinations except those near 0° and 180°. The peak near 0° is due to the large number of Jupiter family comets.
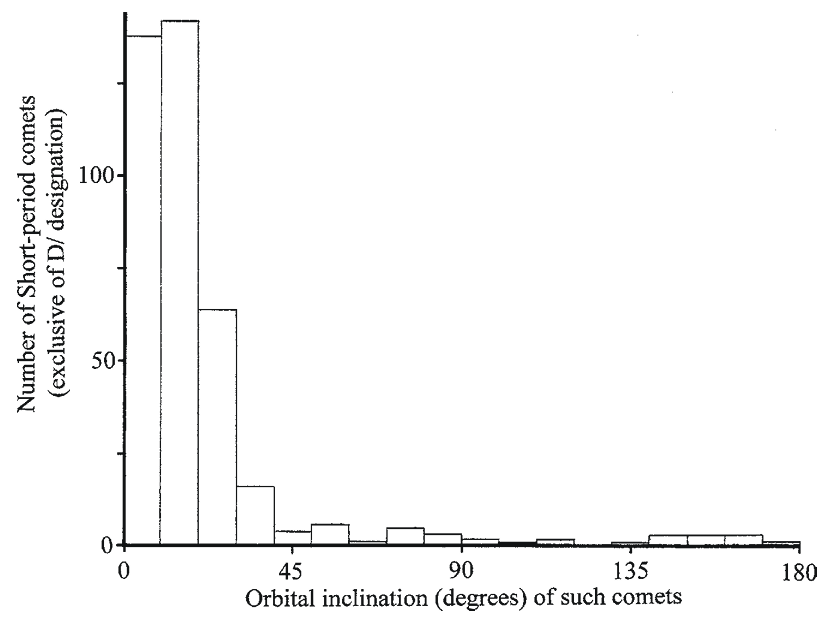
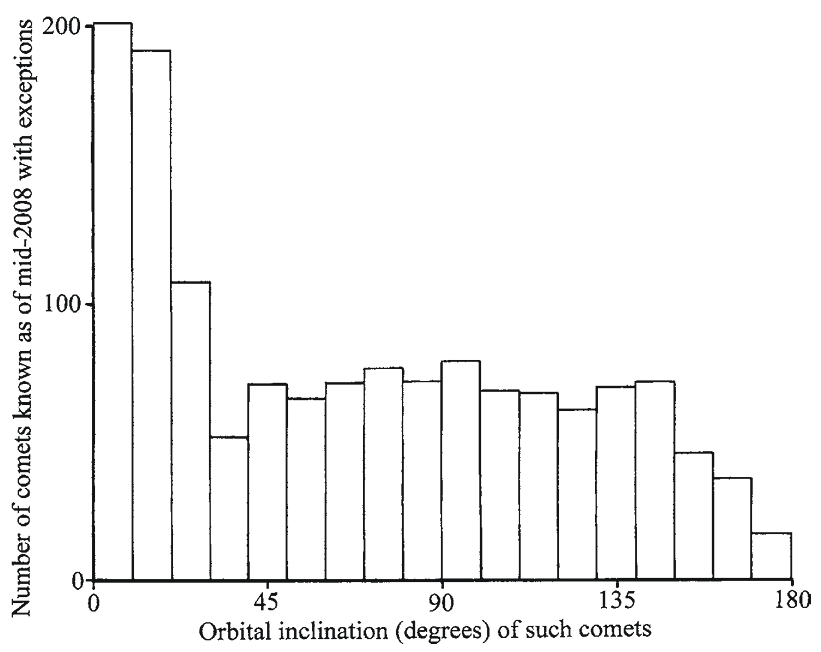 Left
LeftFig. 1.30
Except for short-period comets with a D/ designation, this graph shows the number of all other Short-period comets with different orbital inclinations. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Right
Fig. 1.31
This graph shows the different orbital inclinations of all comets known as of mid-2008 except those named SMM, SOHO, SOLWIND, STEREO and those with a D/ designation. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit all: Richard W. Schmude Jr.)
all from Schmude (2010)
Does Fig. 1.31 [right] give an accurate picture of comet inclinations? Probably. Over the past few centuries, technology has played an important role in changing our view of the Universe. Major technological breakthroughs or advances in photography, digital imaging, the Internet and space probes have occurred. During the latter part of the nineteenth century, photography was developed to the point where it was used successfully in astronomy. Comet Barnard 3 (D/1892 T1) was the first comet discovered with photography. Since then, astronomers have discovered dozens of comets with this technique. During the late twentieth century, digital cameras, the SOHO space probe and the internet have allowed astronomers to discover over 1,000 new comets. In fact, more comets were discovered between 2000 and 2008 than in the previous 2,000 years. In essence, our understanding of comets and the distribution of their orbital inclinations have changed as a result of technological advances. Therefore, in an attempt to answer the question posed, our knowledge of comet inclinations as of 1892 and 1989 is presented below.
- from Schmude (2010:28-29)
- the number of comets with orbital inclinations below 30° which is about average compared to those with inclinations between 30° and 160°
- the number of comets with an orbital inclination above 160° which is below average.
Figure 1.33 [Middle] shows the distribution of orbital inclinations of all known comets as of December 31, 1989 except for comets named SMM, SOHO, SOLWIND and those with a D/ designation. There is a higher than normal abundance of comets with orbital inclinations below 30° in Fig. 1.33 [Middle] than with inclinations above 30°. There is also a definite drop of comets with orbital inclinations over 160°. Therefore, the first trend in Fig. 1.32 [Left] did not hold the test of time, but the second one did. By 1989, it was apparent that orbital inclinations were not evenly distributed. Figure 1.31 [Right] shows the distribution of orbital inclinations up to mid-2008. The trend of low orbital inclinations held up between 1989 and 2008. The scarcity of comets with orbital inclinations above 160° is still apparent in 2008. This trend was evident in 1892.
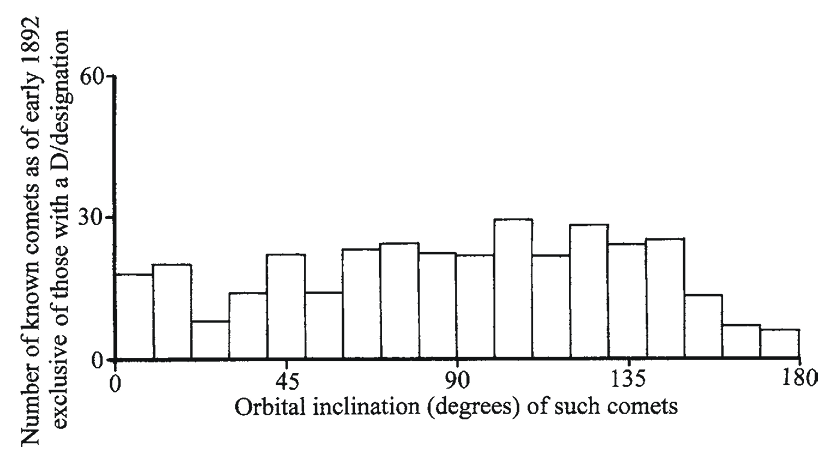
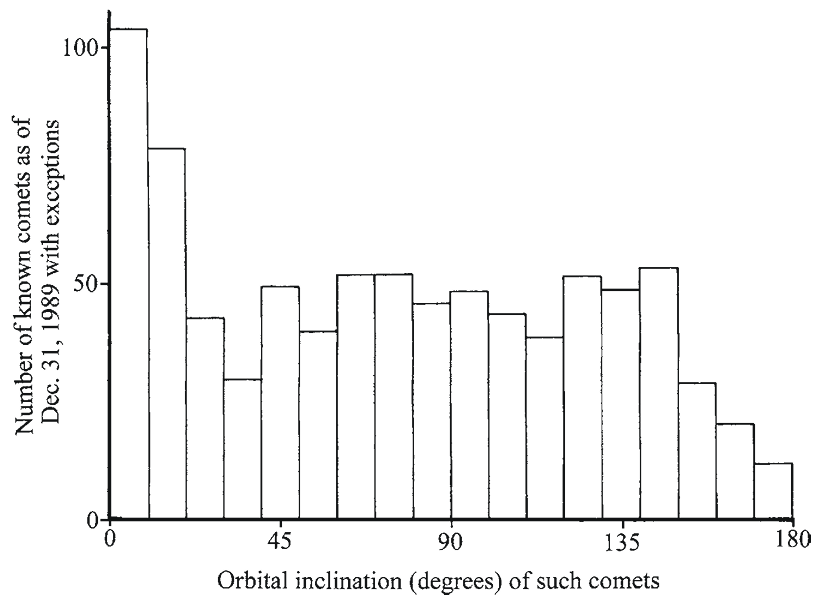

Fig. 1.32
This graph shows the number of comets known as of 1892 (excluding those with a D/ designation) with different orbital inclinations. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Middle
Fig. 1.33
This graph shows the number of comets with different orbital inclinations. All comets known as of December 31, 1989 are included except those named SMM, SOHO, SOLWIND, and those with a D/ designation. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Right
Fig. 1.31
This graph shows the different orbital inclinations of all comets known as of mid-2008 except those named SMM, SOHO, SOLWIND, STEREO and those with a D/ designation. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit all: Richard W. Schmude Jr.)
all from Schmude (2010)
- from Schmude (2010:30)
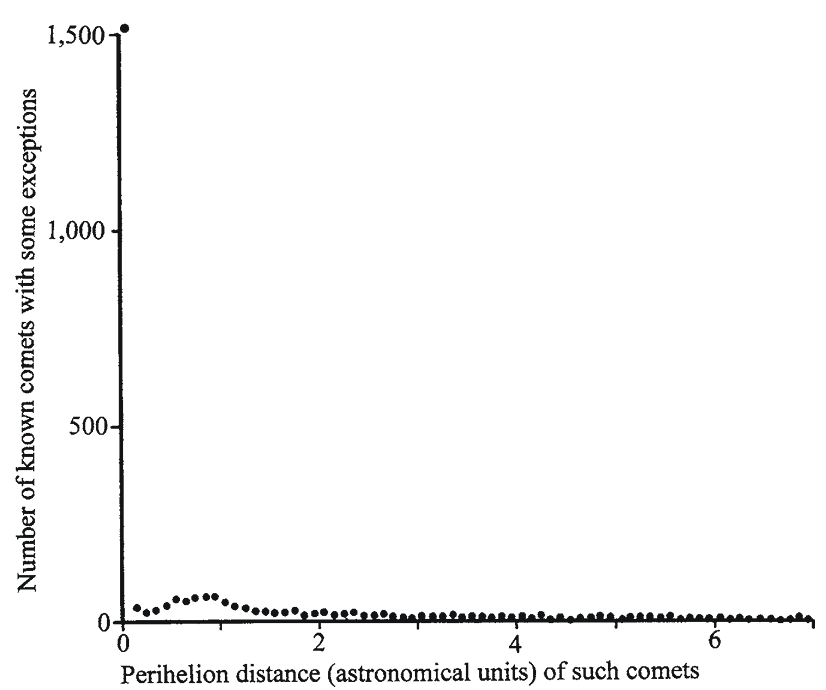

Fig. 1.34
This graph shows the number of comets with different values of the perihelion distance. It includes all known comets as of mid 2008 except those with perihelion distances exceeding 7.0 au and those with a D/ designation. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
Right
Fig. 1.35
This graph shows the number of comets with different perihelion distances. It includes all comets known as of mid-2008 except for those with perihelion distances exceeding 7.0 au, those named SMM, SOHO, SOLWIND and STEREO and those with a D/ designation. Data are from Catalogue of Cometary Orbits 2008, 17th edition ©2008 by Brian G. Marsden and Gareth V. Williams
(credit all: Richard W. Schmude Jr.)
all from Schmude (2010)
- from Schmude (2010:30-36)
When a comet is far from the Sun, it loses its coma. All that is left of the comet is its bare nucleus. It is always very faint. Its brightness, in stellar magnitudes, follows (1.4).
V filter brightness = V(1,0) + 5 log[r*Δ] + Cv*α (1.4)In this equation, V(1,0) is the absolute nuclear magnitude in a filter transformed to the Johnson V system, r and Δ are the comet-Sun and comet-Earth distances in astronomical units, Cv is the solar phase angle coefficient, in units of magnitudes/ degree, and α is the solar phase angle in degrees. The solar phase angle is the angle between the Sun and the observer measured from the target which, in this case, is the nucleus. The solar phase angle coefficient varies with different nuclei. Ferrín (2005, 2007) reports values of the solar phase angle coefficients for ten nuclei ranging from 0.025 magnitudes/degree up to 0.063 magnitudes/degree.
The absolute nuclear magnitude, V(1,0), is the brightness of the nucleus, in stellar magnitudes, when that object is 1.0 au from both the Earth and the Sun and is at a full phase. The value of V(1,0) depends on the size of the nucleus and on its albedo. The albedo is the fraction of light that an object reflects compared to the total amount of light falling on it. If we assume that comet nuclei have nearly the same albedo, the value of V(1,0) would be a measure of the size of the nucleus. One group of astronomers has compiled values of absolute nuclear magnitudes for 118 different Jupiter family comets. Most of the absolute nuclear magnitude values fall between 15 and 18. The average absolute nuclear magnitude is 16.7, with a standard deviation of 1.3 stellar magnitudes.
Once a nucleus begins developing a coma, (1.4) is no longer applicable. The brightness depends on both the nucleus and the coma. At this point, the comet’s brightness depends on its distance from both the Earth and Sun, along with the size and density of the coma. Any sudden event, such as an explosive release of gas and dust, will affect also the brightness. When a comet begins developing a coma, its brightness will depend on both the nucleus and the coma. Once a large coma develops, the nucleus has almost no effect on the comet’s brightness. At this point, (1.5) and (1.6), below, are used to describe comet brightness.
Mc = H10 + 5*log[Δ] + 10*log[r] (1.5)In (1.5), Mc is the measured comet magnitude made visually and corrected to a standard aperture of 6.8 cm, H10 is the normalized magnitude which is the brightness in stellar magnitudes that the comet has if it is 1.0 au from both the Earth and Sun, Δ is the comet-Earth distance, and r is the comet-Sun distance. Both r and Δ are in astronomical units. In (1.6), 2.5n is an adjustable parameter and H0 is the normalized magnitude for a given value of 2.5*n, and the other quantities are the same as in (1.5). The term 2.5*n in (1.6) is called the pre-exponential factor. Equation (1.5) has only one adjustable parameter (H10) whereas (1.6) has two adjustable parameters (H0 and2.5*n). An example of the evaluation of H0 and 2.5*n is presented in Chap. 3.
Mc = H0 + 5*log[Δ] + 2.5*n*log[r] (1.6)
If one uses a photoelectric photometer or a CCD camera with a filter trans formed to the Johnson system then (1.5) and (1.6) should be re-written as:
Vc = V10 + 5*log[Δ] + 10*log[r] (1.7)In these equations, Vc is the V filter brightness of the coma in stellar magnitudes, V10 and V0 are the normalized magnitudes based on Vc values. The Δ, n and r terms are the same as in the original (1.5) and (1.6). It is important for people to distinguish between brightness measurements with the eye versus those made with calibrated filters.
Vc = V0 + 5*log[Δ] + 2.5*n*log[r] (1.8)
Figure 1.36 [Left] shows the distribution of H10 values for 350 comets (not including numbered periodic comets) appearing between 1801 and 1959. The average H10 value for these comets is 7.01. The distribution of H10 values appears to match a standard bell curve with a standard deviation of around two stellar magnitudes. Essentially the data in this Figure are consistent with the average comet shining at magnitude 7.01 when it is 1.0 au from the Earth and Sun.
Figure 1.37 [Middle] shows the distribution of normalized magnitude, H0, values based on (1.6), and Fig. 1.38 [Right] shows the distribution of pre-exponential factor, 2.5*n values. Both figures are based on H0 and 2.5*n values of 127 numbered Short-period comets. The average H0 value is 9.70 with a standard deviation of about two stellar magnitudes. The average value of the pre-exponential factor, 2.5*n (1.6) is 13.9, with a standard deviation of about five stellar magnitudes. This value is somewhat larger than the assumed value of 2.5*n = 10 or n = 4 in (1.5).

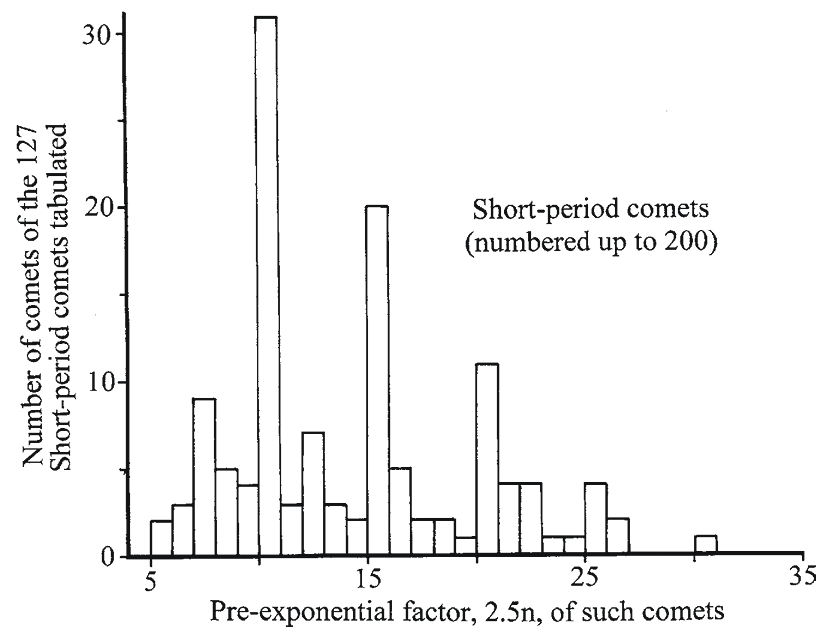
Fig. 1.36
This graph shows the distribution of H10 values (1.5) for 350 comets studied between 1801 and 1959. Numbered periodic comets are not included. Data are from Cometography, Volumes II through IV ©2003, 2007 and 2009 by Gary Kronk. These values have not been corrected for aperture
Middle
Fig. 1.37
This graph shows the distribution of normalized magnitude (H0 ) values for 127 numbered Short-period comets. Most of the values are from the International Comet Quarterly, Vol. 28, No. 4a and Vol. 2, No. 4a. Some of the data came from Jonathan Shanklin’s website, The Comet’s Tail newsletter (written by Jonathan Shanklin) and the author’s analysis of a few comets. All of the values are believed to have been corrected to a standard aperture of 6.8 cm
Right
Fig. 1.38
This graph shows the distribution of pre-exponential factor (2.5n) values for 127 numbered Short-period comets. Most of the values are from the International Comet Quarterly, Vol. 28, No. 4a and Vol. 2, No. 4a. Some of the data came from Jonathan Shanklin’s website, The Comet’s Tail newsletter (written by Jonathan Shanklin) and the author’s analysis of a few comets. All of the values are believed to have been corrected to a standard aperture of 6.8 cm
(credit all : Richard W. Schmude Jr.)
all from Schmude (2010)
Figure 1.39 [Left] shows the distribution of normalized magnitude (H0) values for certain Long-period comets, and Fig. 1.40 [Right] shows the distribution of pre-exponential factor (2.5*n) values for certain Long-period comets. Both figures are based on values from 181 comets. The average H0 value for these comets is 7.49 stellar magnitudes, and the average value of the pre-exponential factor is 9.16.
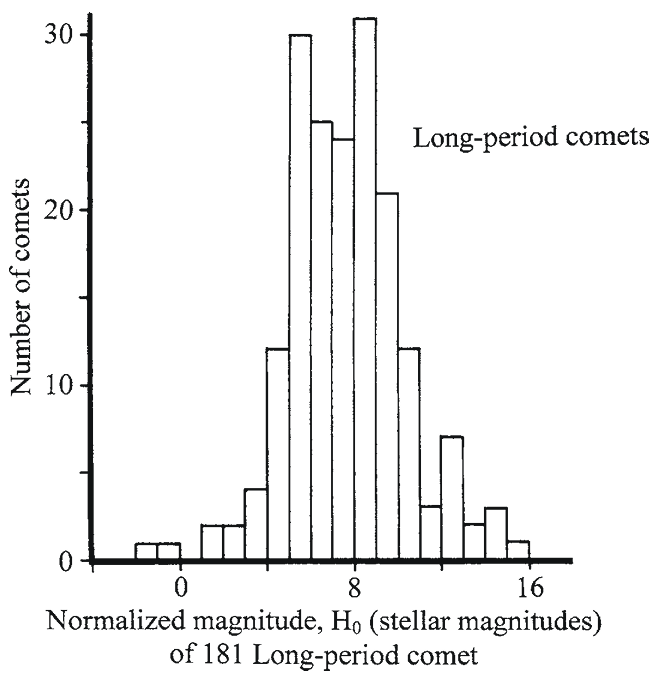
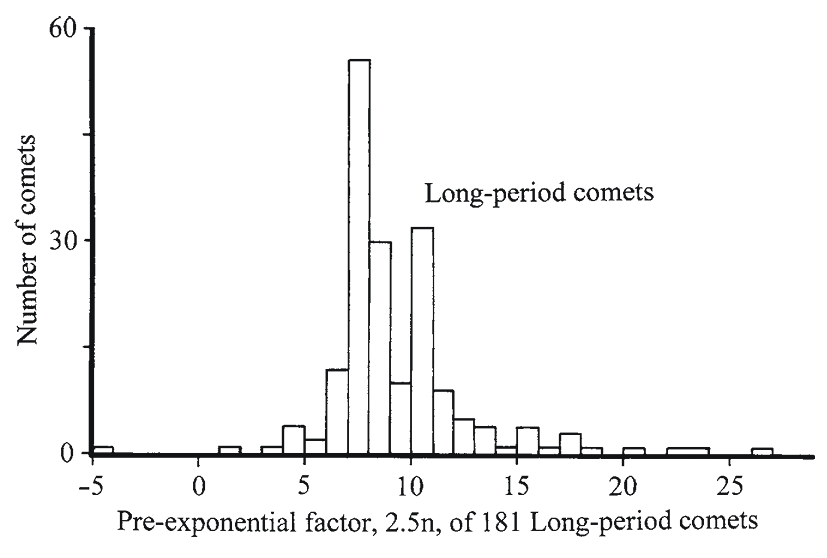
Fig. 1.39
This graph shows the distribution of normalized magnitude (H0 ) values for 181 Long-period comets. Most of the values are from the International Comet Quarterly, Vol. 28, No. 4a and Vol. 2, No. 4a. Some of the data also came from Jonathan Shanklin’s website, The Comet’s Tail newsletter (written by Jonathan Shanklin), the Journal of the Association of Lunar and Planetary Observers and the author’s analysis of a few comets. All of the values are believed to have been corrected to a standard aperture of 6.8 cm
Right
Fig. 1.40
TThis graph shows the distribution of pre-exponential factor (2.5n) values for 181 Long-period comets. Most of the values are from the International Comet Quarterly, Vol. 28, No. 4a and Vol. 2, No. 4a. Some of the data also came from Jonathan Shanklin’s website, The Comet’s Tail newsletter (written by Jonathan Shanklin), the Journal of the Association of Lunar and Planetary Observers and the author’s analysis of a few comets. All of the values are believed to have been corrected to a standard aperture of 6.8 cm
(credit all: Richard W. Schmude Jr.)
all from Schmude (2010)
Table 1.7 summarizes the average values of H0, 2.5*n and H10 for numerous short- and long-period comets. One difference between these two groups of comets is that the H0 and H10 values are about two to three magnitudes fainter for the short period comets than long-period comets. This may be due to short-period comets having lost most of their volatile substances due to their many past close encounters with the Sun. There is also a sizable difference in the 2.5*n values for short period comets and long-period comets. This difference may be due to the short-period comets having less highly-volatile substances compared to those with long periods.
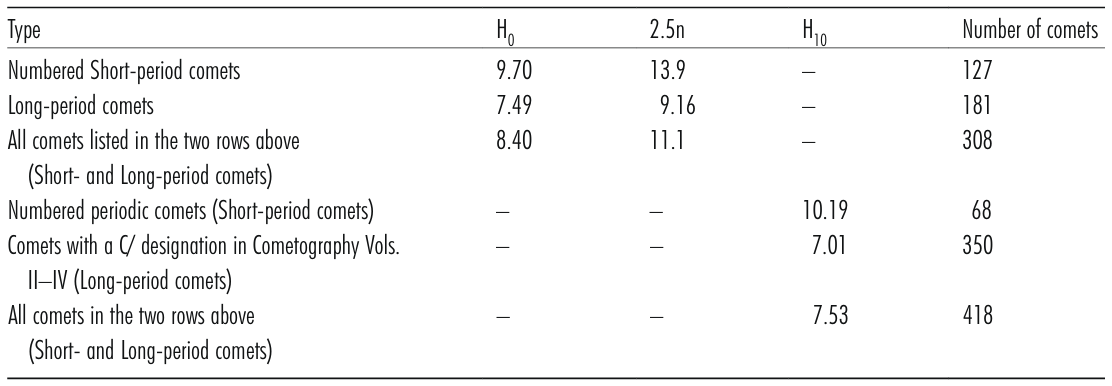 Table 1.7
Table 1.7Average values of H10, H0 and 2.5n in (1.5) and (1.6) for large groups of Short- and Long-period comets. These values have been computed by the writer using values compiled from several sources including the International Comet Quarterly, The Journal of the Association of Type Lunar and Planetary Observers, Jonathan Shanklin’s Website, The Comet’s Tail newsletter (written by Jonathan Shanklin) and the author’s analysis of a few comets
Schmude (2010)
Can the H0 value tell us anything about the size of the nucleus? This is a difficult question to answer. A preliminary discussion is presented below. In this regard, note first that Table 1.8 lists characteristics of a few short-period cometary nuclei. These characteristics are based on spacecraft images. The comet with the largest nucleus in the table, 1P/Halley, has the smallest H0 value, which is what should be expected. After all, the largest nucleus should have the largest coma and, hence, reflect the largest amount of light. The comet with the smallest nucleus, 81P/Wild 2, has the largest H0 value and, hence, its coma reflects the smallest amount of light of the four comets listed.
 Table 1.8
Table 1.8Characteristics of the nuclei of four comets. The sources for the areas of the nuclei are listed in Tables 2.2, 2.5, 2.12 and 2.15. The author computed the H0 values from data reported in the International Astronomical Union Circulars and a few issues of the International Comet Quarterly
Schmude (2010)
Furthermore, I have computed the logarithm of the areas of the cometary nuclei listed in Table 1.8. The abbreviation for logarithm is log. The log[area in km2] values and the H0 values in Table 1.8 were fitted to a linear least squares equation. The result:
Log(nucleus area in km2) = 3.99 - 0.327*H0 Short period comets (1.9)The data follow this (1.9) well. The correlation coefficient, r, for (1.9) equals 0.96. This equation was used to generate approximate areas and diameters of nuclei of Short-period comets with different values of H0. These results are summarized in Table 1.9 and may be useful in answering the question posed.
 Table 1.9
Table 1.9Values of the area, equivalent diameter and the logarithm of the area of nuclei of Short-period comets based on (1.9) in the text. The author computed the values in this table using (1.9) in the text
Schmude (2010)
Finally, it is believed that (1.9) and Table 1.9 should be considered as a very preliminary answer to the question posed. There are several factors that one should consider when relating H0 values to the size of cometary nuclei. Three of these are
- the fraction of the surface of a nucleus which is active
- the amount of dust released during the release of volatile substances
- the particle size distribution of dust released.
- from Schmude (2010:44-)
Astronomers have measured the loss rate of water and other gases for several comets. A typical loss rate for water is 3 × 1028 molecules per second. If this loss rate is sustained for 3 months, 2.3 × 1035 H2O molecules would be lost which would be equivalent to 7 × 109 kg. On a spherical nucleus that has a diameter of 4 km, this would be equivalent to a layer that is 140 cm (or 55 in.) deep if spread over 10% of the surface of the nucleus. Due to this fact, a nucleus can produce a coma for dozens of trips around the Sun, provided that its volatile-rich deposits are at least 100-m deep and the perihelion distance is greater than about 0.6 au.
There are other factors which affect comet brightness which need consideration. Brightness is affected by comet-Sun and comet-Earth distances. For this reason, a normalized magnitude, such as H10, must be considered instead of the comet’s actual brightness. This is because the normalized magnitude is the brightness of a comet when it is 1.0 au from both the Earth and Sun. As a result, different distances do not change the H10 value. See (1.5).
Mc = H10 + 5*log[Δ] + 10*log[r] (1.5)A second factor is the uncertainty in the brightness measurements. Measurements made with the eye have an uncertainty of 0.5 magnitudes, whereas those made with a photometer or a CCD camera may have an uncertainty of 0.01 magnitudes. Naturally, brightness measurements with small uncertainties are more likely to reveal long-term changes.
Lots of data over a wide range of comet-Sun distances are needed to compute H0 values. This data is often not available. For this reason, I concentrated on H10 values. In most cases, my aim has been to look for brightness changes over the last 100 years.
Common sense dictates that comets showing the first sign of fading should be those that have short orbital periods. Accordingly, I have examined several comets with short orbital periods, i.e. those with orbital periods less than 200 years. One problem with older H10 values is that they are not corrected to a standard aperture of 6.8 cm. To make matters more complicated, astronomers in the 19th and early 20th centuries made most of their visual brightness estimates with refractors. Since the 1960s, astronomers have made most of their brightness estimates with Newtonian reflectors. Newtonian reflectors have a much smaller aperture correction factor than refractors of the same diameter. For example, a 0.25 m (10 in.) refractor has an aperture correction factor of −1.2 stellar magnitudes, whereas the same-sized Newtonian reflector has a correction factor of only −0.3 stellar magnitudes. As a result, it is believed that all H10 comet values, with the exception of 1P/Halley, should be corrected to a standard aperture of 6.8 cm. Since most of the H10 values for Comet 1P/Halley are based on data collected before the invention of the telescope, the H10 values based on unaided-eye estimates deviates only slightly form one apparition to the next.
I have considered nine periodic comets in the analysis. One of those, 2P/Encke, has been studied already, and its results are quoted without modification. With corrected brightness, the estimates of comets 4P/Faye, 6P/d’Arrest, 7P/Pons-Winnecke, 8P/ Tuttle, 10P/Tempel 2, 19P/Borrelly and 81P/Wild 2 are corrected to a standard aper ture of 6.8 cm. If the aperture was not obvious for a brightness estimate it was not used. I did not use photographic magnitudes because photographic plates are more sensitive to blue light than human eyes. Once normalized magnitudes, H10, were computed I then computed linear equations relating the H10 values to the year. Figures 1.45–1.48 show the results for the comets 6P/d’Arrest, 7P/Pons-Winnecke, 19P/Borrelly and 81P/Wild 2.
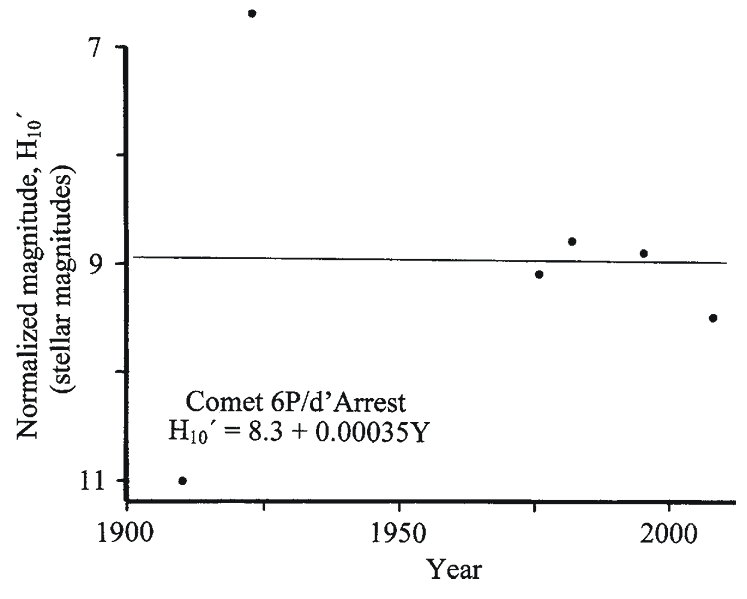
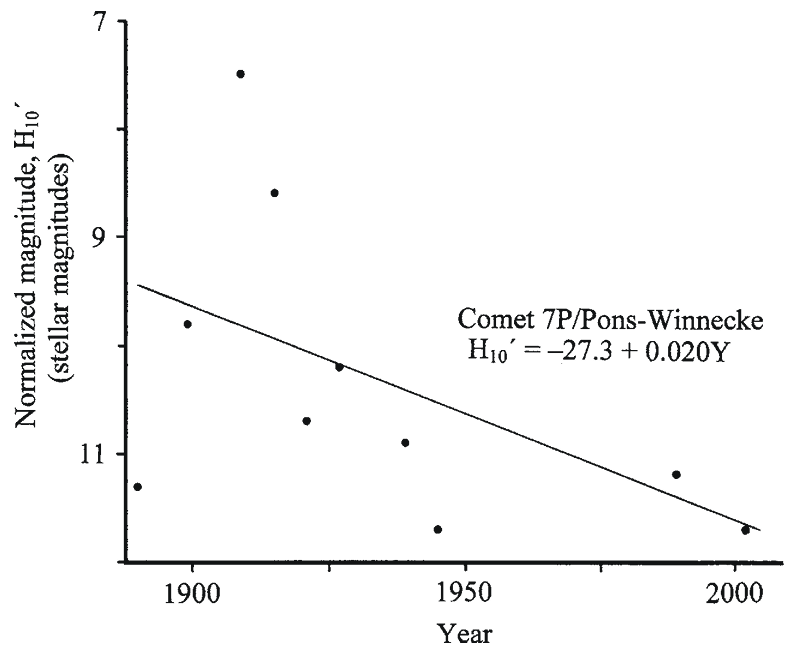
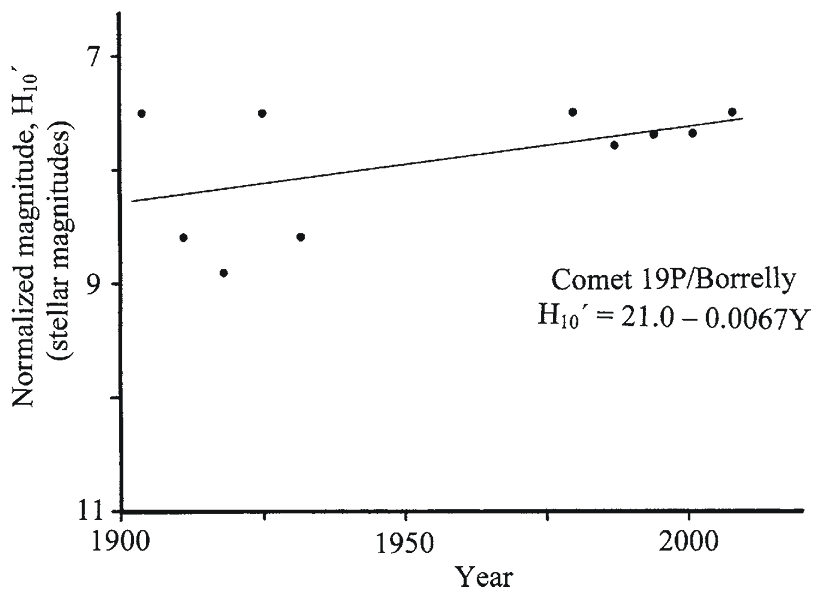
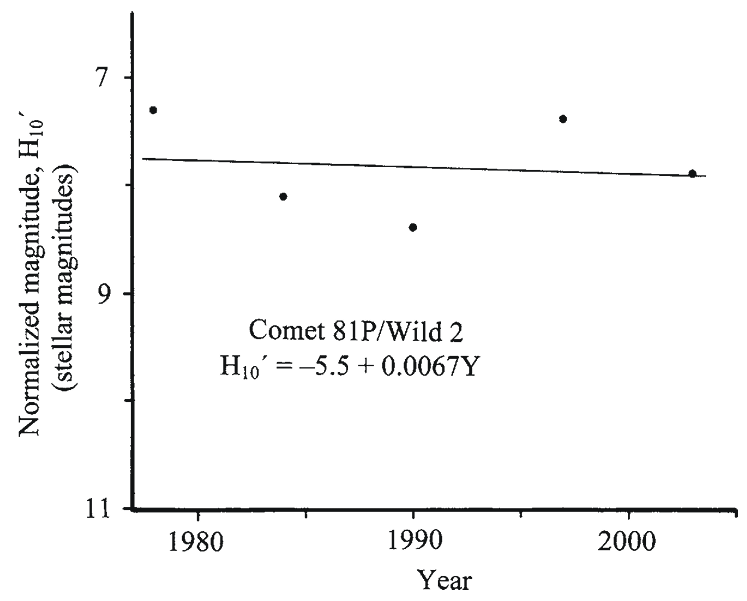
Fig. 1.45
This graph shows a linear fit to the H10 ¢ values of Comet 6P/d’Arrest between 1910 and 2008. Data before 1933 are based on brightness estimates reported in Cometography vol. III ©2007 by Gary Kronk which have been corrected to a standard aperture of 6.8 cm. Data after 1974 are from an analysis by the author of measurements reported in IAU Circulars. The author corrected these data to a standard aperture of 6.8 cm. In the equation, Y is the yearMiddle Left
Fig. 1.46
This graph shows a linear fit to the H10 ¢ values of Comet 7P/Pons-Winnecke measured between 1892 and 2002. Data before 1959 are based on brightness estimates reported in Physical Characteristics of Comets ©1964 by S. K. Vsekhsvyatskii and Cometography vol. II and III © 2003, 2007 by Gary Kronk which have been corrected to a standard aperture of 6.8 cm. Data after 1974 are from an analysis by the author of measurements reported in IAU Circulars and are corrected by him to a standard aperture of 6.8 cm. In the equation, Y is the year
Middle Right
Fig. 1.47
This graph shows a linear fit to the H10 ¢ values of Comet 19P/Borrelly measured between 1904 and 2008. Data before 1934 are from Cometography vol. III ©2007 by Kronk. Data after 1974 are from an analysis by the author of measurements reported in IAU Circulars and corrected by him to a standard aperture of 6.8 cm. In the equation, Y is the year
Far Right
This graph shows a linear fit to the H10 ¢ values of Comet 81P/Wild 2 measured since 1978. All data are from an analysis by the writer of measurements reported in IAU Circulars. The author corrected the data to a standard aperture of 6.8 cm. In the equation, Y is the year
(all credit: Richard W. Schmude Jr.)
all from Schmude (2010)
In each of these figures, a linear equation is given which relates the normalized magnitude to the year – Y. In the case of comets 4P/Faye, 7P/Pons-Winnecke and 81P/Wild 2, the normalized magnitude value increases with time. This means that these comets grew fainter over the time increment covered by the data. The normalized magnitude of Comet 7P/Pons-Winnecke, for example, dimed at an average rate of 0.02 stellar magnitudes/year during the twentieth century. Comets 10P/Tempel 2 and 19P/Borrelly, on the other hand, grew brighter during most of the twentieth century. The change in the brightness of Comet 6P/d’Arrest, for example, is so small that it is considered negligible.
Table 1.12 summarizes the relationship between the normalized magnitude, H10', and year for nine periodic comets. Four of the comets show little or no change in their H10' value over time, that is, the brightness change is less than 0.001 magnitudes/year. Three of them have a dimming trend in their H10' values, while two have a brightening trend. When the results are averaged, these comets dimmed at a rate of 0.003 magnitudes/year. This rate however is well below the standard deviation for the nine brightness change values of 0.009 magnitudes/year.
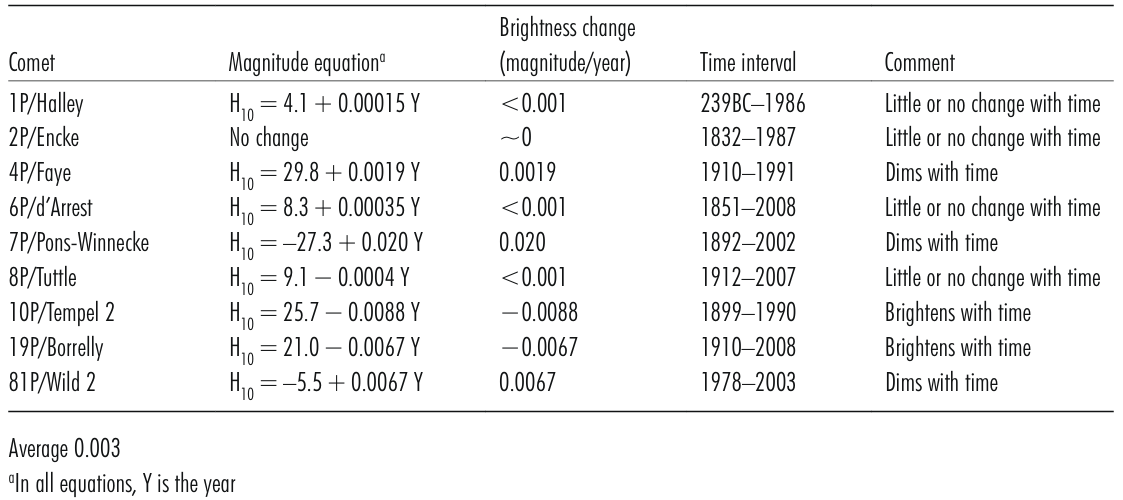 Table 1.12
Table 1.12A summary of changes in the H10 values and brightness for nine periodic comets over time. The author computed the H10 values from data in the International Astronomical Union Circulars, the International Comet Quarterly and Cometography, Volumes I–III ©1999, 2003 and 2007 by Gary Kronk
Schmude (2010)
Table 1.13 shows the data in Table 1.12 in terms of the comet’s orbital period. When taken together, the average change in the normalized magnitude is 0.026 stellar magnitude (or about 2%) per orbit for all nine comets.
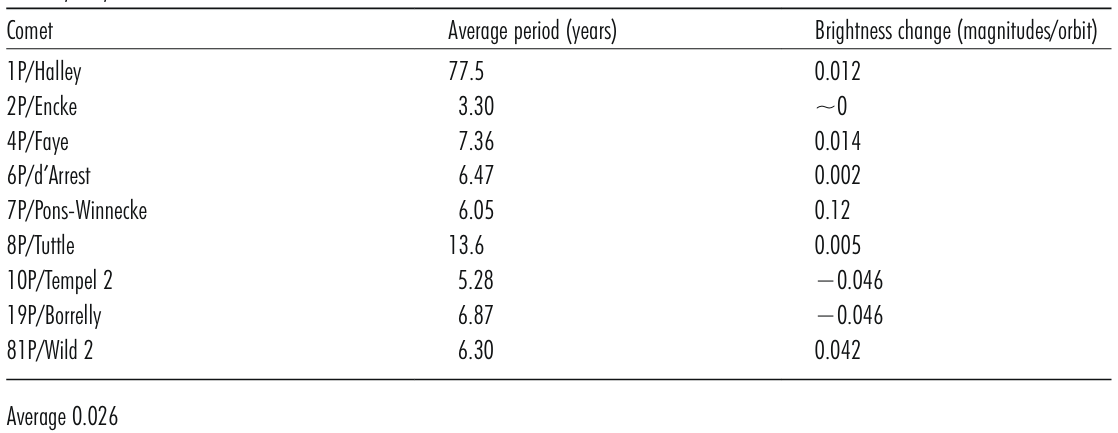 Table 1.13
Table 1.13A summary of changes in the brightness per orbit for nine periodic comets over time. The author computed the H10 values from data in the International Astronomical Union Circulars, the International Comet Quarterly and Cometography, Volumes I–III ©1999, 2003 and 2007 by Gary Kronk.
Schmude (2010)
Since the average normalized magnitude value has a slight increase in time, it is a sign of dimming. The scatter in the data, however, prevents me from making a reliable conclusion for these comets. Meisel and Morris (1982) examined 11 periodic comets and concluded that there is little or no dimming taking place over time.
One way to address the question of comet dimming in the future is to make brightness estimates with CCD cameras and standard filters. Such measurements should contain the entire coma. One can attain an accuracy of 0.01 stellar magnitudes with CCD measurements. Highly accurate magnitude measurements made over a few decades will serve as a powerful tool in the search for long-term brightness changes in periodic comets.