CHRONOS
Ancient Chronology Calculators
Calculators Coded by Jefferson Williams combined with External Calculators not coded by JW
Roman Numerals Converter
from romannumerals.co
from romannumerals.co
Julian Day
Julian Day Calculations allow you to figure out the day of the week.
| Hour (0-24) |
Day | Month | Year | Local Longitude |
Specify E or W Longitude 1 - East 2 - West |
Standard Julian Day (12 hour UT) |
Local Julian Day |
Weekday |
|---|---|---|---|---|---|---|---|---|
Hover over underlined variables for pop up explanations. The calculator above computes Julian Day and day of the week for the Julian and Gregorian calendars and is valid from noon 1 January 4713 BCE until present. In these calendars, a new day begins at midnight. Lunar and lunisolar local calendars (e.g., Islamic, Hebrew, Syriac, and Coptic Liturgical Calendars) start their day at night fall and solar calendars (e.g., Coptic Civil Calendar) start their day at sunrise. Make adjustments to the day of the week accordingly (see illustration below).
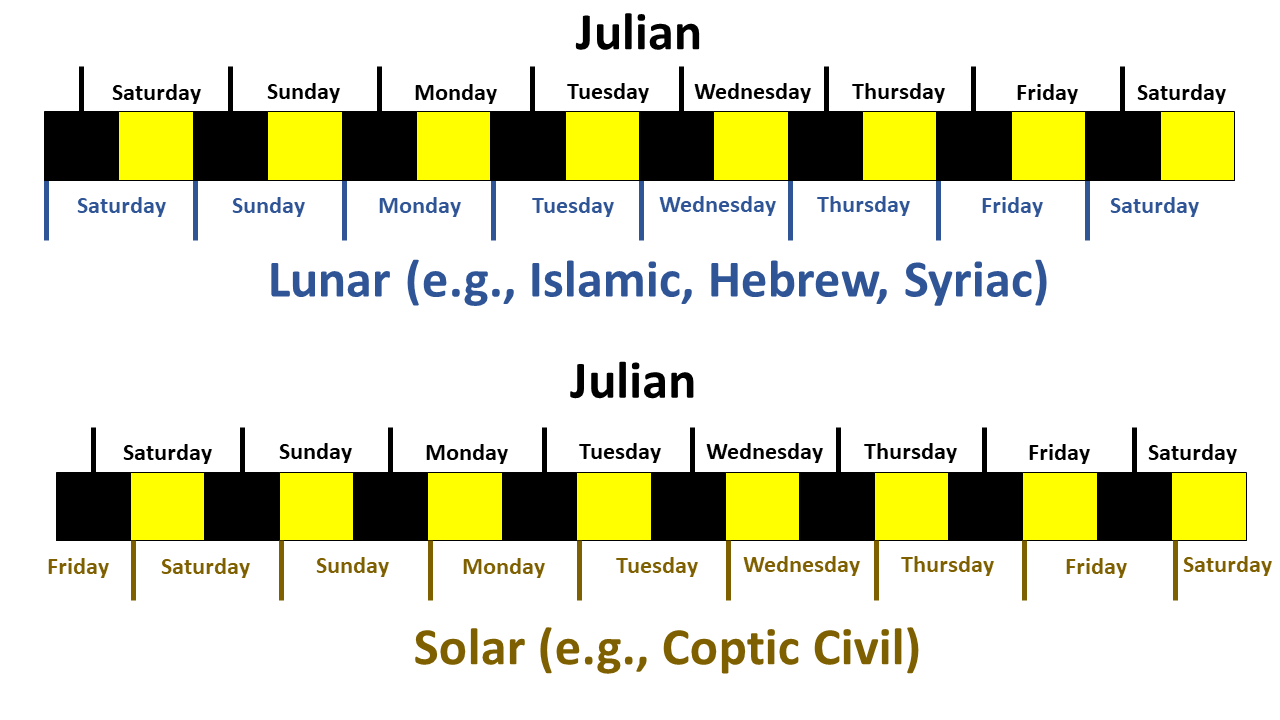 Days of the Week in different calendars
Days of the Week in different calendarsillustration by Jefferson Williams
Meeus, J. (1991). Astronomical algorithms. Richmond, Virginia USA, Willmann-Bell Inc., pages 60-65
timeprophecy.com - makes a nice detailed calculation of JD, Day of Week, Moonrise, Moonset, Sunrise, Sunset, etc. and is seamlessly valid for Julian and Gregorian calendar time periods
fourmilab computes JD - fourmilab computes Julian Day at UT zero hour (not 12). It has seperate entry forms for the Julian and Gregorian Calendars.
- The Julian Day starts at 0.0 at noon on 1 January 4713 BCE (-4712 in astronomical years)
The Julian Day number or, more simply, the Julian Day (JD) is a continuous count of days and fractions thereof from the beginning of the year —4712. By tradition, the Julian Day begins at Greenwich mean noon, that is, at 12h Universal Time. If the JD corresponds to an instant measured in the uniform scale of Dynamical Time, the expression Julian Ephemeris Day (JDE) is often used. For example,
1977 April 26.4 UT = JD 2443 259.9In the methods described below, the Gregorian calendar reform is taken into account. Thus, the day following 1582 October 4 (Julian calendar) is 1582 October 15 (Gregorian calendar).
1977 April 26.4 TD = JDE 2443 259.9
The Gregorian calendar was not at once officially adopted by all countries. This should be kept in mind when making historical research. In Great Britain, for instance, the change was made as late as in 1752, and in Turkey not before 1927.
...
There is a disagreement between astronomers and historians about how to count the years preceding the year 1. In this book, the "B.C." years are counted astronomically. Thus, the year before the year +1 is the year zero, and -the year preceding the latter is the year —1. The year which the historians call 585 B.C. is actually the year —584. (Do not use the mention "B.C." when using negative years! " —584 B.C.", for instance, is incorrect.) [JW: This is accounted for in the Calculator so one should enter historical years]
The astronomical counting of the negative years is the only one suitable for arithmetical purposes. For example, in the historical practice of counting, the rule of divisibility by 4 revealing the Julian leap years no longer exists; these years are, indeed, 1, 5, 9, 13, ... B.C. In the astronomical sequence, however, these leap years are called 0, -4, -8, —12 , and the rule of divisibility by 4 subsists.
...
take care when using the INT function for negative numbers.
...
The week was not modified in any way by the Gregorian reform of the Julian calendar. Thus, in 1582, Thursday October 4 was followed by Friday October 15.
...
When is a given year a leap year ?
In the Julian calendar, a year is a leap (or bissextile) year of 366 days if its numerical designation is divisible by 4. All other years are common years (365 days).
For instance, the years 900 and 1236 were bissextile years, while 750 and 1429 were common years.
The same rule holds in the Gregorian calendar, with the following exception : the centurial years that are not divisible by 400, such as 1700, 1800, 1900, 2100, are common years. The other century years, which are divisible by 400, are leap years, for instance 1600, 2000, and 2400.
| Location | Approx. Longitude |
|---|---|
| Cairo | 31.3 |
| Jerusalem | 35.3 |
| Beirut | 35.5 |
| Antioch | 36.2 |
| Damascus | 36.3 |
| Edessa (Sanliurfa) | 38.8 |
| Mabbug (Manbij) | 38.0 |
| Baghdad | 44.4 |
| Tabuk | 36.6 |
| Medina | 39.6 |
| Mecca | 39.8 |
Julian to Gregorian
The Gregorian Calendar went into effect in October 1582 CE. It was adopted by various countries and entities after this date - replacing the earlier Julian Calendar. One notable holdout is the Greek Orthodox Church which still uses the Julain Calendar.
from fourmilab
Anno Mundi (A.M.)
A.M. – Anno Mundi. This calendar was used by several of the Byzantine authors including Theophanes and Anastasius Bibliothecarius. The calendar is based on the Julian calendar however the year does not begin on 1 January and the starting day, month, and year of this calendar was a point of contention as it was based on an estimate for the start of "creation" (among other things) as interpreted through the Septuagint - a Greek translation of the Old Testament. An ongoing several hundred year long theological debate over when Biblical "creation" began led to multiple versions of the A.M. calendar. The earlier Byzantine sources used the Alexandrian version (A.M.a) or “Alexandrian era” of this calendar which has a starting date of 25 March 5492 BCE or, according to Bickerman (1980), 25 March 5493 BCE. Earthquake catalogers Guidoboni et al (1994) and Ambraseys (2009) assume a starting date of 25 March 5492 BCE and that is what I use. As explained by Grumel (1958:219)
The Alexandrian era of Panodorus began in 5493 BCE [and] the Alexandrian era of Annianos began in 5492 BCE. The Alexandrian Era of Annianos is what is commonly called the Alexandrian era.Another reckoning system, used for example by Megas Chronographos, is the Byzantine version (A.M.Byz) which has a starting date of 1 September 5509 BCE (Bickerman, 1980:73-74). Yet another reckoning system is a variant suggested in Chronicon Paschale which was composed in ~630 CE. The starting date for this system is 21 March, 5507 BCE. In the Anno Mundi calendar system used by the Byzantine authors, the day followed the Roman civil custom of beginning the calendarical day at midnight. When hours are indicated they mark time since dawn. Hence, if daybreak began at 6 am, the 4th hour would correspond to 10 am (Rautman, 2007:3).
Calendaric Inconsistencies of Individual Authors
| Author | Inconsistencies | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Theophanes | Theophanes used the Alexandrian version of the Anno Mundi calendar even though it was out of favor at the time and would be obsolete by the 9th century CE. He did so because his
Chronicle was a continuation of George Syncellus Chronicle which itself used the Alexandrian version of the Anno Mundi calendar. Proudfoot (1974:374)
noted that the problem of whether Theophanes regarded the year as commencing on March 25 according to the Alexandrian world-year or on September 1 according to the Byzantine indiction cycle has not been resolved with [] clarity. |
||||||||||||||||||||||||||||||
| Theophanes |
Grumel (1934:407),
Proudfoot (1974:373-374), and others have pointed out that Theophanes A.M.a
in the years A.M.a 6102-6206 and A.M.a
6218-6265 are frequently a year too low. The indictions, however, are thought by many more likely to be correct.
The indiction runs from Sept. 1st, the Alexandrian A.M. from March 25th, but Theophanes probably dates the latter for calendar purposes from Sept. 1st2, to correspond with the Indiction. |
Alexandrian fully QCed, Byzantine partly QCed and Chronicon Pachale not QCed
| Enter A.M. Year | Specify Reckoning 1 - Alexandrian 2 - Byzantine 3 - Chronicon Paschale |
Chosen Reckoning | Time Span in the Julian Calendar |
|---|---|---|---|
Indictions
Indictions - An indiction (Latin: indictio, impost) was a periodic reassessment of taxation in the Roman Empire which took place every fifteen years.
In Late Antiquity, this 15-year cycle began to be used to date documents and it continued to be used for this purpose in Medieval Europe. Indictions
refer to an individual year in the 15 year cycle; for example, "the fourth indiction" came to mean the fourth year of the current indiction. Since
the cycles themselves were not numbered, other information is needed to identify the specific year. When an ancient author supplies an indiction along
with an A.M. date, the result may be greater chronological precision. For our dating purposes, indictions began in 312 CE when they were introduced by the Roman Emperor
Constantine. The indiction was first used to date documents unrelated to tax collection in the mid-fourth century.
By the late fourth century it was being used to date documents throughout the Mediterranean.
In 537 CE, Roman Emperor Justinian decreed that all dates must include the indiction.Outside of Egypt, the year of the indiction generally began on 1 September
(Bickerman, 1980:78).
| Input | Start Year (CE) | Notes |
|---|---|---|
| Invalid before 312 CE | ||
| Indiction | Year (CE) | Indiction Time Span outside of Egypt |
Regnal Years
| Regnal Year | Start Day | Start Month | Start Year (CE) | Time Span in the Julian Calendar |
|---|---|---|---|---|
Seleucid Era including the Syriac Calendar (A.G. - Anno Graecorum)
The Anno Graecorum (A.G.) Calendar is also known as the Seleucid Era, Chaldean, or the
Macedonian Calendar.
This calendar began at the start of the Seleucid Empire and was
assimilated into the Babylonian calendar with Macedonian month-names sometimes substituted for the Babylonian names (Stern, 2012:238). The A.G. calendar uses the same
19 year cycle of intercalations as the Babylonian calendar. There are two start dates. The Macedonian reckoning used
by court officials in the Seleucid Empire and native Greek speakers started in the Autumn of 312 BCE with the start date eventually getting fixed
to 1 Oct. 312 BCE. The Babylonian reckoning used by most Semitic speaking populations has a start date of 1 Nisan in 311 BCE. Ambraseys (2009) equates this
to 1 April, Guidoboni et al (1994) equate this with 2 April, and others equate it to 3 April. A version of the A.G. calendar was used by the Christian Syriac authors such as Pseudo-Dionysius of Tell Mahre
and Chronicon Ad Annum 1234. Syriac writing authors would have likely used the
Macedonian reckoning as this was the standard usage among these authors for the Seleucid era (Sebastian Brock, personal communication, 2021 – see also Stern, 2012:236).
In the Anno Graecorum calendar system, the day starts at sundown (Sebastian Brock, personal communication, 2022).
| Macedonian Month | Julian Equivalent | Duration (days) |
|---|---|---|
| Xanthikos | 22 March - 20 April | 29 |
| Artemisios | 21 April - 20 May | 30 |
| Daisios | 21 May - 19 June | 29 |
| Panemos | 20 June - 19 July | 30 |
| Loos | 20 July - 18 Aug. | 29 |
| Gorpiaios | 19 Aug. - 17 Sept. | 30 |
| Hyperberetaios | 18 Sept. - 17 Oct. | 29 |
| Dios | 18 Oct. - 16 Nov. | 30 |
| Apellaios | 17 Nov. - 16 Dec. | 29 |
| Audynaios | 17 Dec. - 15 Jan. | 30 |
| Peritios | 16 Jan. 14 Febr. | 29 |
| Dystros | 15 Febr. - 16 March | 30 |
| Epagomenai | 17 March - 21 March | 5 |
| Enter A.G. Year | Specify Reckoning 1 - Macedonian 2 - Babylonian |
Chosen Reckoning | Time Span in the Julian Calendar |
|---|---|---|---|
Islamic (A.H. - Anno Hegirae)
A.H. – Anno Hegirae is also known as the Muslim Calendar or the Islamic lunar calendar. The start date is the Hijra - when on Friday 16 July 622 CE, Mohammed and his followers
migrated from Mecca to Medina. The calendar consists of 12 alternating months of 30 and 29 days. Although the original calendar determined the start of each month based
on astronomical observation of the first visible crescent after a new moon, a fixed tabular calendar was developed in the 8th century CE. In the tabular calendar,
a day is added to the final (12th) month during leap years making it 30 days long instead of 29. Leap days are added every 2-3 years in a 30 year cycle which is
subject to local variation. The most common distribution is on the 2nd, 5th, 7th, 10th, 13th, 16th, 18th, 21st, 24th, 26th, and 29th year of each 30-year cycle (timeanddate.com).
The Islamic day begins at sundown.
from fourmilab
Coptic (A.M. - Anno Martyrum)
The Coptic Calendar is also known as the Alexandrian Calendar. The Coptic Calendar is coordinated with the Julian Calendar and, since the 4th century CE, used a
starting year (Year 1) from 29 August 284 CE to 28 August 285 CE. A year consists of 13 months where the first 12 months have 30 days each followed an epagomenal
month which has 5 days during normal years and 6 days during leap years. This version of the Coptic calendar is frequently called the Era of Martyrs and is
frequently abbreviated as A.M. (Anno Martyrum). Coptic Leap Years are coordinated with Julian leap years however the coptic leap day is added on the last day
of the coptic year rather than on 29 February. If a Coptic year will encompass a Julian Leap year (i.e. a year where there will be a February 29),
the coptic year will start on 30 August instead of 29 August as 29 August in the previous Coptic year will be a leap day. In years such as this, the
coptic day will be a day ahead of the Julian Calendar until 29 February. Thus, for example while 21 Tuba normally corresponds to 16 January, in a Julian Leap Year
it will correspond to 17 January. The Coptic day begins at sunrise in the civil calendar and sunset in the liturgical version
(Claremont Coptic Encyclopedia).
from Episteme Academy
The Coptic Calendar - Claremont Coptic Encyclopedia
The Coptic Calendar - timeanddate.com
The Coptic Calendar - wikipedia (has a great Coptic Months Table)
The Coptic Calendar by Bishoy Dawood
Converts from Julian to Coptic and other calendars
Chaine, M. (1925). La chronologie des temps chrétiens de l'Égypte et de l'Éthiopie. Paris, P. Geuthner.
The Coptic Calendar (info)
The Coptic Calendar of Martyrs at copticchurch.net
Hebrew
The Hebrew Calendar is also known as the Jewish Calendar or HaLuah HaIvri (הַלּוּחַ הָעִבְרִי) in Hebrew. The Hebrew Calendar is a lunisolar calendar influenced by the Ancient
Babylonian Calendar which has undergone revisions over time. Initially, this calendar was based on sightings of the first crescent after the new moon. After the
destruction of the 2nd temple in 70 CE and throughout the diaspora, the calendar was subject to local variations. By the 4th century CE, a calendar had emerged
which was increasingly based on predicted lunar cycles. Sometime before the 8th century, a fixed 19 year Metonic cycle of intercalations similar to the Babylonian
cycle was adopted and by the early 10th century, the rabbinic calendar had become like the fixed and predictable calendar that is used today. (Stern, 2012:334-335),
The structure of the Hebrew Calendar is one of 12 months with an additional intercalary month added in years 3, 6, 8, 11, 14, 17, and 19 of the
Metonic cycle along with a complicated set of rules (Reingold and Dershowitz, 2018:Section 8.1).
The modern Hebrew Calendar is also characterized by a change in the start date of the calendar from the destruction
of the second Temple in 70 CE to the start of “creation”
like the Anno Mundi Calendar of the Byzantines.
In the Hebrew Calendar, the day begins at sundown.
4.4.1 The Present-Day Rabbinic Calendar: An Outline
- The conjunction (molad) is calculated on the basis of two values
- the mean lunation (duration of the lunar month) of 29 days, 12 hours, and 793 parts (there are 1080 parts to an hour).
- molad of Tishre year 1 (of the era of creation, i.e. the first Tishre in ‘history’), which is given as 2nd day (Monday), 5 hours (of the 24-hour period beginning in the evening), 204 parts, or in its Hebrew acronym: (BaHaRaD). This corresponds to Sunday, 6 October 3761 BCE at 23 hours, 11 minutes, and 20 seconds (assuming the day begins at 18 hours). The molad of Tishre year 1 functions as an epoch (reference point). Any subsequent molad can be worked out by adding the right number of lunations to this epoch. As an alternative to BaHaRaD, the molad of the following Tishre (year 2) can also be used. This molad is 6th day (Friday), 14 hours, no parts (acronym: WeYaD).The fact that this epoch is a round figure (with no parts of the hour) suggests that this was the original epoch to have been in use.
- The month begins, apriori, on the day of the molad. Sometimes it is postponed by one or more days, because of the rules that follow (iii–iv), which are hence known as ‘postponement’ rules.
- Rosh ha-Shanah, 1 Tishre, cannot occur on Sunday, Wednesday, on Friday. This rule is known by its Hebrew mnemonic: (lo ADURosh). If the molad of Tishre occurs on any of these days, the 1st of the month must be postponed.
- If the molad of Tishre occurs on or after the 18th hour (i.e. midday), the 1st of the month must be postponed. (footnote: If the following day is either Sunday, Wednesday, or Friday, Rosh ha-Shanah must be postponed till the day after, hence a postponement of two days.) This is known as molad zaqen (‘late conjunction’).
- The calendar consists of a fixed alternation of 29 and 30 day months: there are always 30 days in Nisan, 29 days in Iyyar, etc. Only the months of Marḥeshwan and Kislew are subject to variation: they can be ‘regular’ (i. e. 29–30), ‘full’ (i.e. 30–30), or ‘defective’ (i.e. 29–29) . This variation makes it possible for rules (iii) and (iv) to be observed, i.e. for the subsequent Rosh ha-Shanah(s) (sometimes more than one year ahead) not to occur on the wrong days. This variation also makes it possible to compensate for the discrepancy between the mean lunation under rule (i)(a) and the average month length of 29½ days resulting from a pure alternation of 29- and 30-day months.
- The intercalation is based on a fixed 19-year cycle, which starts at year 1 (from the creation) and within which the following seven years are intercalated: 3, 6, 8, 11, 14, 17, 19. Intercalation consists of an additional 30-day month, which is inserted before Adar and called ‘first Adar’
from fourmilab. This converter uses modern Hebrew Calendar rules
fourmilab converts from the Hebrew calendar to the Julian Calendar and vice-versa
Episteme Academy web page Converts from the Julian Calendar to Coptic calendar
The Hebrew Calendar - wikipedia
Stern, S. (2001). Calendar and Community: A History of the Jewish Calendar, 2nd Century BCE to 10th Century CE..
.
Seasonal Drift of the Hebrew Calendar
Hebrew Calendar Calculator
Era of Province Arabia
The Era of Province Arabia (also called Bostran era, the era of Bostra, the Arabian era, or Provincial era) was a calendar era
(year numbering) with an epoch (start date) corresponding to 22 March 106 AD. It was the official era of
the Roman province of Arabia Petraea, introduced to replace dating by regnal years after the Roman
annexation of the Nabataean Kingdom. The Bostran era is named after the city of Bostra, which became the
headquarters of the Sixth Legion stationed in the province.
| Enter Year of Province Arabia | Time Span in the Julian Calendar |
|---|---|
Olympiads (Ol.)
The Era of the Olympiads was widely used in ancient texts and is based on the Greek Olympiads which were held every four years. The start date of this calendar is accepted by most modern scholars as 1 July 776 BCE (Finegan, 1998:93). Olympiads (abbreviated Ol.) are four years apart with 4 cycles specifying years within the Olympiad.
| Enter Olympiad Year | Enter Olympiad Cycle (1-4) | Time Span in the Julian Calendar |
|---|---|---|
Melkite Era of the Incarnation
Treiger (2015) describes this as follows:
6. The Melkite Era of the Incarnation
The honor of discovering the Melkite era of the Incarnation (AInc), in use from the eleventh to the fourteenth century, belongs to Samir Khalil Samir (Samir 1987). By looking at Melkite colophons where dates “to the divine Incarnation” (li-l-taǧassud al-ilāhī) are given alongside dates according to other eras, he discovered that AInc dates are 8-9 years ahead of AD dates. The conversion key is as follows:
1 January–31 August: AInc–8 = AD;
1 September–31 December: AInc–9 = AD.
Bibliography
Samir, Samir Khalil. “L’ère de l’Incarnation dans les manuscrits arabes melkites du 11e au 14esiècle.” Orientalia Christiana Periodica 53 (1987): 193-201
| Enter Melkite Year | Time Span in the Julian Calendar |
|---|---|
Year of the Incarnation (aka Divine Incarnation Year)
The year of the Incarnation was occasionally used by Syncellos/Theophanes and Anastasius Bibliothecarius (when copying from Theophanes ?). It has a start date of 9 CE (Martin, 1930:12). This calculator is based on the assumption that year 1 of the divine incarnation year was from 25 March 9 to 24 March 10 CE which equates to A.M.a 5501 (Adler and Tuffin, 2002:lxxi-lxxiv). This is what Syncellos used. Absent further investigation, I cannot guarantee that Theophanes and Anastasius Bibliothecarius rigorously applied this calculation methodology.
Adler and Tuffin (2002:lxxi-lxxiv) discuss Syncellos use of this dating system as follows:
(c) Years from the Incarnation
For Synkellos, the Incarnation refers to Jesus' conception in the womb, not his birth. His initial promise to prove that the Incarnation of Christ occurred in AMa 5500 is somewhat imprecise. When he later addresses this matter in more depth, he refines this statement: the conception of Jesus occurred at the completion of AM 5500, on the first day of AM 5501 (= 25 March).191 Since Synkellos follows the era of Annianos, this would translate into AD 9 (5501 - 5492 = 9).192 After establishing this date, Synkellos provides years from the divine Incarnation, alongside universal years. He calculates these years by subtracting 5500 complete years from the universal year. The following table gives a brief overview of Synkellos' system; note that the equivalences are those which ought to obtain whether or not they actually do in his calculations:193
Footnotes191 Synk. 377i25-378.4 381.5-22.
192 Synkellos states that Africanus also dated the birth of Christ to 5500. But since Africanus' universal era was different from Annianos', the year 5500 in Africanus' chronicle does not translate into the same year of the Christian Era. The year 5500 in Africanus' chronicle equates with 2 BC, not AD 9.
193 This is particularly true of the relations between his Olympic years and the regular reckoning given in the table. In fact, Synkellos seems to be using as many as three Olympiad eras: 01. 1.1 is AM 4721 at -131.3-4, 4719 at 234.12-13, and 4725 at 23 3.7-8.




194 This is the correct date, but Synkellos gives variously AM 4719 = 774 BC(234.13) AM 4725 = 768 BC (233.7-8),
and (apparently) AM 4726 = 767 BC (235.22).
195 See remarks prefacing this table.
196 So Synkellos; according to Eusebios (PE Io.IO.IO) Africanus dated the Exodus
1237 years before i Cyrus (= AM 3705).
197 Synkellos actually gives the Olympiad date as 01. 187.4 (379.29.
191 According to other witnesses Africanus dated the Crucifixion to 5532; see
below, p. 471 n. 2.
199 Except for the dates of 01. 1.1 and the Nativity, imported from Eus.-Jer.
Canons. The Olympiad dating derived from Synkellos' does not always coincide with
the dates found in other versions of Eusebios' chronicle. Note too that while
Synkellos usually gives Eusebian dates in years from Adam, Eusebios' more
customary practice is to count from Abraham; hence an additional column is needed
giving dates according to the Abrahamic era. Reflecting Synkellos' own practice, the
count of years from Abraham does not include his first year.
| Enter Incarnation Year | Time Span in the Julian Calendar |
|---|---|
Year of Abraham (Anno Abraham) - used in Eusebius' Chronicle
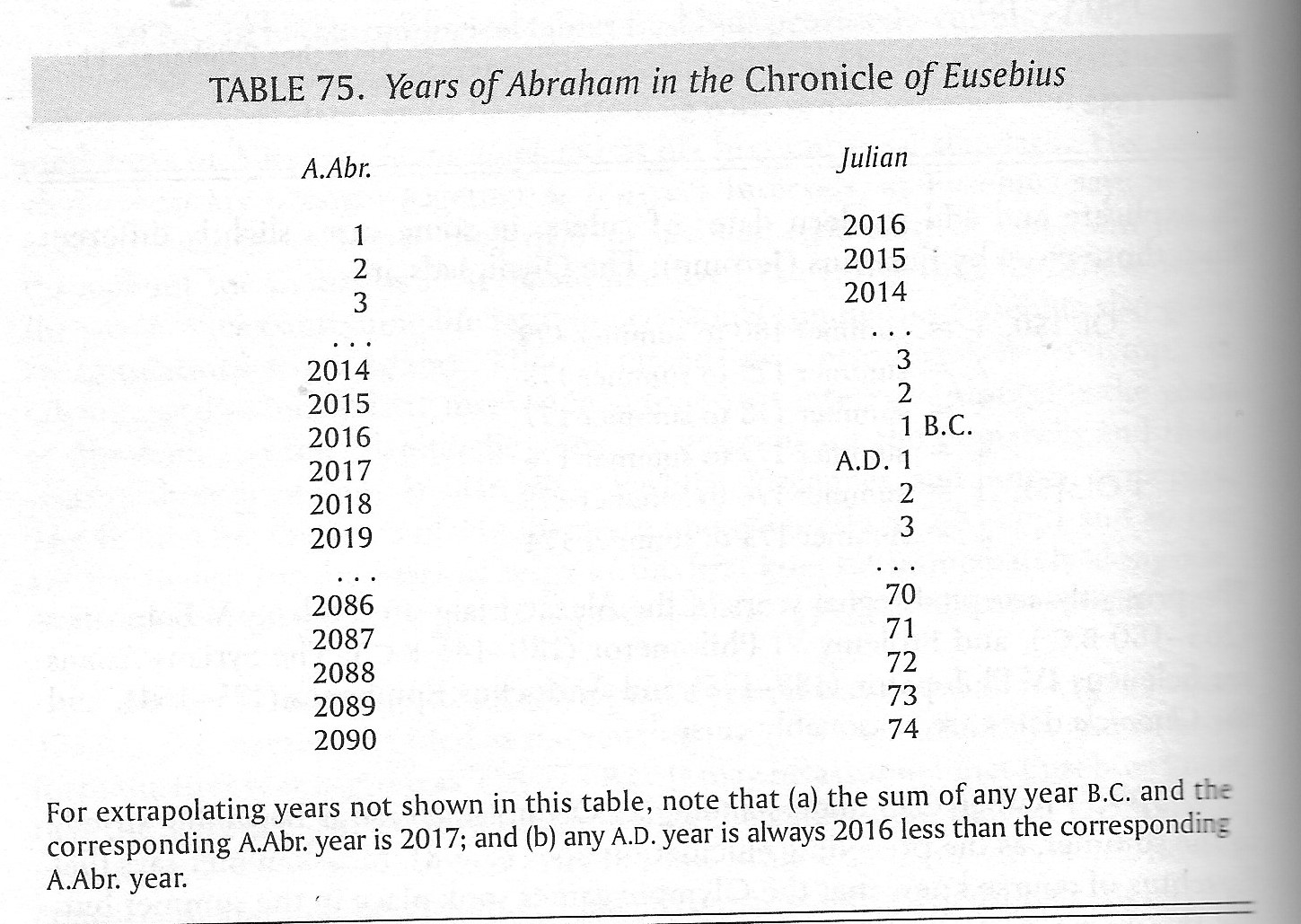
Finegan (1998) describes the Year of Abraham as follows
With regard to the years of Abraham in Helm's edition of the Chronicle of Eusebius: like the Olympiadic dates (§308), the Abrahamic dates are stated in single-year figures but are to be understood as overlapping two years. Thus the generally accepted date of the first year of Abraham, which is marked as equivalent to 2016 B.C.,98 is to be understood as 2016/2015 B.C.; and the further years of Abraham in our Table 75 are all to be understood in the same way." The correctness of the initial dates of 776/775 B.C. for the sequence of Olympiadic years (§308 Table 46) and of 2016/2015 B.C. for the sequence of years of Abraham (§309 Table 75) in the Chronicle of Eusebius (Jerome) will be confirmed at the place where the Chronicle comes to a well-known point in Babylonian and biblical chronology, namely, the second year of the Persian king, Darius I (§§330-333, Tables 89, 90). Theoretically an overlap could be either forward or backward; e.g., the year A.D. 68 could mean either 68/69 or 67/68 (cf. §671).
For extrapolating years not shown in this table, note that (a) the sum of any year B.C. and the corresponding A.Abr. year is 2017; and (b) any A.D. year is always 2016 less than the corresponding A.Abr. year.
Footnotes
98 Helm20a-20b.
| Enter Year of Abraham | Time Span in the Julian Calendar |
|---|---|
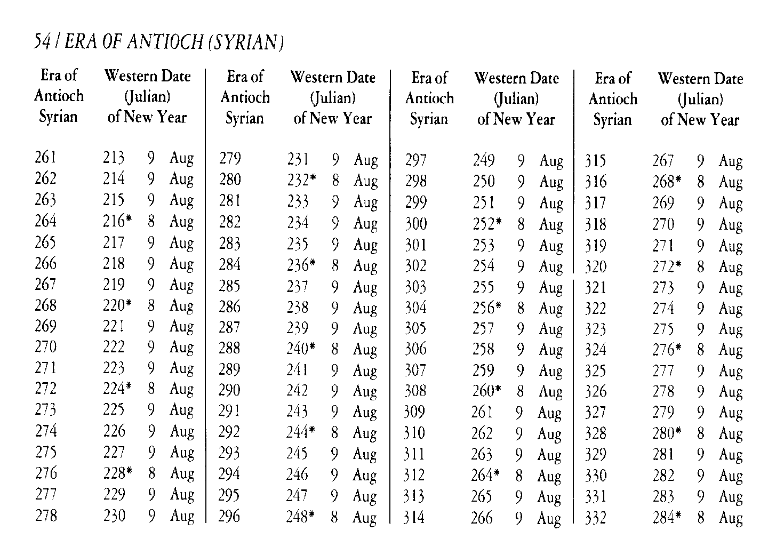
Antiochene Year - used by Malalas
Malalas defined the start of Era of Antioch in Book 9 [217] of his Chronicle.
Gaius Julius Caesar entered Antioch on the 23rd day of the month of Artemisius; he constructed a basilica, which he called the Caesarium, opposite the temple of Ares that was afterwards called the Macellum, and there he erected a bronze statue to the Fortune of Rome. He also constructed, on the so-called acropolis in the upper part of Antioch the great, public baths for the use of the inhabitants of the acropolis; he brought the water for the baths [217] from the spring of the Laodicean Way, along an aqueduct that he constructed. And there in the upper part [of the city] he constructed an arena for gladiators and a theatre; he also restored the Pantheon, which was about to collapse, and erected an altar.Downey (1963:283) dates Julius Caesar's visit to Antioch to 47 BCE. Julius Caesar was assassinated on 15 March 44 BCE.
Then this Caesar went off to Alexandria the great and constructed there, naming it after his son by his beautiful concubine Cleopatra - he found this Cleopatra in the Thebaid, where she had been banished by her brother Ptolemy, who was hostile towards her; Caesar seduced [Cleopatra] and made her pregnant; and she bore a son, whom she called Caesarion - so Julius Caesar constructed the Caesarium in Alexandria the great, naming it after his own son. He expelled Cleopatra's brother Ptolemy from the kingdom of Egypt, and gave the kingdom of Egypt to Cleopatra, after killing the two eunuchs who had persuaded Ptolemy to banish her to the Thebaid. But the son of Cleopatra and Caesar died while he was still young.
When Caesar returned to Rome, he was murdered by the second Brutus and the other senators who conspired with him, in the consulship of (?) Isauricus and Antonius (for the second time). Therefore the first year of the era of Antioch the great is counted from this year, in honour of Gaius Julius Caesar.
In discussing the Trajan Quake, Ambraseys (2009:123) equates the Antiochene Year of 164 with October 115 - September 116 CE where a typo appears to have reduced his reference to the number 116. In discussing an Earthquake in 458 CE in Antioch, Ambraseys (2009:169) equates the Antiochene Year of 506 with 1 October 457 to 30 September 458. For now, this calculator is based on these calibration points which seem to date Julius Caesar's visit to Antioch to between 1 Oct. 49 BCE and 30 Sept. 48 BCE, differing with Downey (1963:283).
Parise (2002) defines the Era of Antioch a year later than Ambraseys (2009:123, 169) and also has different start and end dates. A summary for few different years is provided below:
| Era of Antioch Greek | New Years Day (Julian) | Era of Antioch Syrian | New Years Day (Julian) |
|---|---|---|---|
| 1 | 4 Sept. 48 BCE | 1 | 9 Aug 48 BCE |
| 32 | 5 Sept. 17 BCE | 32 | 8 Aug 48 BCE |
| 48 | 8 Aug 1 BCE | ||
| 49 | 9 Aug 1 CE | ||
| 332 | 5 Sept. 284 CE | 332 | 8 Aug 284 BCE |
Downey (1961) dates the founding of Antioch by the Seleucids to May 300 BCE and the founding of Seleucia Piera to April 300 BCE.
| Enter Antiochene Year | Time Span in the Julian Calendar |
|---|---|
Ambraseys, N. (2009). Earthquakes in the Mediterranean and Middle East: a multidisciplinary study of seismicity up to
1900. Cambridge, UK, Cambridge University Press.
Glanville Downey, A. (1961). History of Antioch in Syria from Seleucus to the Arab Conquest, Princeton Univ. Press, New Jersey, Princeton.
Downey, G. (1963). Ancient Antioch, Princeton University Press.
Parise, F. (2002). The Book of Calendars: Conversion Tables for Ancient, African,
Near Eastern, Indian, Asian, Central American and Western Calendars Gorgias Press.
Armenian Era
The wikipedia entry for the Armenian Calendar provides the following:
- The Armenian calendar is based on an invariant year length of 365 days
- Year 1 of the Armenian calendar began on 11 July 552 of the Julian calendar
- The Armenian calendar is divided into 12 months of 30 days each, plus an additional (epagomenal) five days, called aweleacʿ ("superfluous")
- Years are usually given in Armenian numerals; which are letters of the Armenian alphabet preceded by the abbreviation ԹՎ for t’vin, meaning "in the year." For example, ԹՎ ՌՆԾԵ, which means "the year 1455."
| # | Armenian | H-M Romaniz. |
Meaning | Etymology/Notes |
|---|---|---|---|---|
| 1 | նաւասարդ | nawasard | new year | Avestan*nava sarəδa |
| 2 | հոռի | hoṙi | two | From Georgian ორი (ori) meaning "two" |
| 3 | սահմի | sahmi | three | From Georgian სამი (sami) meaning "three" |
| 4 | տրէ | trē | Zoroastrian Tïr | |
| 5 | քաղոց | kʿałocʿ | month of crops | From Old Armenian քաղեմ (kʿałem) meaning "to gather" from PIE *kʷl̥- |
| 6 | արաց | aracʿ | harvest-time | From old armenian արաց[4](aracʿ), meaning harvest time, harvest of grape/fruit |
| 7 | մեհեկան | mehekan | festival of Mithra | Iranian *mihrakān-; Zoroastrian Mitrō |
| 8 | արեգ | areg | sun month | From Old Armenian արեւ (arew) meaning "sun" from PIE *h₂rew-i- also meaning sun |
| 9 | ահեկան | ahekan | fire festival | Iranian *āhrakān-; Zoroastrian Ātarō |
| 10 | մարերի | mareri | mid-year | Avestan maiδyaīrya; Zoroastrian Dīn |
| 11 | մարգաց | margacʿ | ||
| 12 | հրոտից | hroticʿ | Pahlavi *fravartakān; Zoroastrian Spendarmat̰ | |
| 13 | աւելեաց[5] | aweleacʿ | redundant, superfluous | Epagomenal days |
| # | Name | Armenian Text | Meaning/derivation |
|---|---|---|---|
| 1 | Areg | Արէկ | sun |
| 2 | Hrand | Հրանդ | earth mixed with fire |
| 3 | Aram | Արամ | |
| 4 | Margar | Մարգար | prophet |
| 5 | Ahrank’ | Ահրանկ | half-burned |
| 6 | Mazdeł | ||
| 7 | Astłik | Աստղիկ | Astłik |
| 8 | Mihr | Միհր | Mihr (Armenian deity) |
| 9 | Jopaber | tumultuous | |
| 10 | Murç | Մուրց | triumph |
| 11 | Erezhan | hermit | |
| 12 | Ani | Անի | name of a city |
| 13 | Parkhar | ||
| 14 | Vanat | Վանատ | host, refectioner of a monastery |
| 15 | Aramazd | Արամազդ | Aramazd |
| 16 | Mani | Մանի | beginning |
| 17 | Asak | Ասակ | beginningless |
| 18 | Masis | Մասիս | Mount Ararat |
| 19 | Anahit | Անահիտ | Anahit (Armenian goddess) |
| 20 | Aragats | Արագած | Mount Aragats |
| 21 | Gorgor | Name of a mountain | |
| 22 | Kordvik | 6th province in Armenia Major | |
| 23 | Tsmak | Ծմակ | east wind |
| 24 | Lusnak | Լուսնակ | half-moon |
| 25 | Tsrōn | dispersion | |
| 26 | Npat | Նպատ | Apam Napat |
| 27 | Vahagn | Վահագն | Zoroastrian Vahrām; Avestan Verethragna, name of the 20th day |
| 28 | Sim | Սիմ | mountain |
| 29 | Varag | Վարագ | name of a mountain |
| 30 | Gišeravar | evening star |
from Episteme Academy
Click planetcalc.com link to open calculator in a new tab
Astronomical Calculators
from Clear Sky Tonight - appears to use Julian Calendar prior to 1582 CE
from Clear Sky Tonight - appears to use Julian Calendar prior to 1582 CE
from Clear Sky Tonight - appears to use Julian Calendar prior to 1582 CE
- from imcee
- Note that imcee outputs all dates in the Gregorian Calendar even during the time period when the Julian Calendar was in use.
- Other Calculators at imcee
- from imcee
- Note that imcee outputs all dates in the Gregorian Calendar even during the time period when the Julian Calendar was in use.
- Other Calculators at imcee
Miscellaneous References
Ancient Astronomical Terms
Historical Glossary of Important Terms in Hellenistic Astronomy
Ancient Greek Astronomy and Cosmology
The Precession of the Equinoxes Explained with Graham Hancock - youtube video
Online converters below have not been vetted
Calendarical software
Convert a Date - calendarhome.com
Calendar Utility - www.lieberknecht.de