SEISCALC

Explanation

The attenuation relationship (Eqn. 5 on p. 302) of Hough and Avni (2009) was primarily derived from estimates of inferred local Intensity due to the 1927 M_L 6.25 Jericho Earthquake. It may be less accurate in the far field because news reports were used to infer local Intensity in further afield locations such as Egypt (Amotz Agnon, personal communication, 2020 or 2021).

Calculator

Conversion from Intensity to PGA using Wald et al (1999)
Site Effect not considered

Variable	Input	Units	Notes
Magnitude			Magnitude
R_epi		km.	Distance to earthquake producing fault

I	PGA (m/s²)	Notes	Plot
		Hough and Avni (2009)
		Malkawi and Fahmi (1996) Historical (same formula as "Hussein et al Historical" below, per source)
		Ben-Menahem (1982)
		Hussein et al Historical (same formula as Malkawi and Fahmi (1996) Historical above, per source)
		Boore, Joyner and Fumal (2005; 1981) mod. by Wetzler - models PGA directly, converted to Intensity (and back to PGA) via Wald et al (1999)
		Al-Qaryouti (2008) - models PGA directly (median of the +/-1 sigma bounds), converted to Intensity (and back to PGA) via Wald et al (1999)
		Basket (HA, MF, & AQ) - simple average of Hough and Avni (2009/2011), Malkawi and Fahmi (1996), and Al-Qaryouti (2008)

Copiable summary (click the box to select all, or use the Copy button):

References

Al-Qaryouti, M. (2008). "Attenuation relations of peak ground acceleration and velocity in the Southern Dead Sea Transform region." Arabian Journal of Geosciences 1: 111-117.

Ben-Menahem, A., Vered, M., and Brooke, D. (1982). "Earthquake Risk In The Holy Land." Bollettino di Geofisica Teorica e Applicata XXIV(95).

Darvasi, Y. and Agnon, A. (2019). "Calibrating a new attenuation curve for the Dead Sea region using surface wave dispersion surveys in sites damaged by the 1927 Jericho earthquake." Solid Earth 10(2): 379-390.

Hough, S. E., and Avni, R. (2009). "The 1170 and 1202 Dead Sea Rift earthquakes and long-term magnitude distribution on the Dead Sea fault zone." Israel Journal of Earth Sciences 58(3-4): 295-308.

Husein Malkawi, A. I. and Fahmi, K. J. (1996). "Locally derived earthquake ground motion attenuation relations for Jordan and conterminous areas." Quarterly Journal of Engineering Geology and Hydrogeology 29(4): 309-319.

Lu, Y., et al. (2020). "A 220,000-year-long continuous large earthquake record on a slow-slipping plate boundary." Science Advances 6: 1-10.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Explanations

Wells and Coppersmith (1994) - based on a global dataset

Wells and Coppersmith (1994) compiled a global dataset of historical and instrumental earthquakes and derived empirical scaling relationships that estimate earthquake moment magnitude from observed fault rupture characteristics, including displacement, surface rupture length, subsurface rupture length, rupture area, and fault type (e.g., strike-slip, normal, or reverse faulting). Surface rupture length is the mapped length of faulting visible at the ground surface, whereas subsurface rupture length represents the total rupture length at seismogenic depths. They found that surface rupture length is typically about 75% of subsurface rupture length, although this ratio generally increases with earthquake magnitude. The authors also found that relationships between magnitude and rupture length (surface or subsurface) and rupture area exhibit stronger correlations than those involving displacement, making them generally more reliable predictors of earthquake magnitude. These empirical equations are widely used to estimate the magnitude of prehistoric and historical earthquakes from geological, historical, and archaeological evidence. Numerous alternative scaling relationships have since been proposed using different datasets and statistical approaches.

Ambraseys and Jackson (1998)

For Surface Magnitude (M_S) and Moment Magnitude (M_W) estimates based on Rupture Length (L) in km., Ambraseys and Jackson (1998) presented the following equations:

M_S = 5.13 + 1.14 log(L)        (2)

M_S = 5.27 + 1.04 log(L)        (3)

M_W = 4.9 + 1.33 log(L)         (11)^note

while noting that Equation (3) is almost identical to that derived by Wells and Coppersmith (1994).

Ambraseys and Jackson (1998:397) noted the following

it is important, particularly for palaeoseismological investigations, to have some indication of whether the rupture length and offset estimated from historical sources are likely to be seriously under- or overestimated, given the magnitude of the event. This is a principal use of magnitude—length relationships. For an assessment of individual events or particular regions, it may be more informative to make such estimates from a combination of first principles and more closely constrained empirical relationships, along the following lines:

for earthquakes that rupture the entire thickness (d) of the seismogenic upper crust, the downdip width of the fault is d/sinϴ, where ϴ is the fault dip, and the moment is then

M_o = (μcd/sin ϴ)L²       (8)

where

µ is the rigidity modulus

c is the ratio of average displacement (u) to fault length (L), which is observed to be close to 5 x 10^-5 for intracontinental earthquakes (Scholz 1982; Scholz et al. 1986)

both observationally and theoretically it is known that for such earthquakes the relationship between moment and magnitude (M, whether M_S or M_W ) is of the form

log(M_o)= A + BM       (9)

where A and B are constants, with B ≈ 1.5 (e.g. Kanamori and Anderson 1975; Ekstrom and Dziewonski 1988))

combining these expressions gives a relationship between moment and fault length of the form

M = (1/B) log(µcd/sin ϴ) — (A/B) + (2/B) (log L)       (10)

For illustration, if we take

µ=3 x 10¹⁰ N m^-2

c = 5 x 10^-5

A = 9.0 (for M_o in units of N m, see Ekstrom and Dziewonski 1988)

B=1.5

then for a seismogenic layer of thickness d=15 km and a vertical strike-slip fault (ϴ = 90°), the relationship is

M_W = 4.9+1.33L        (11)

with L in kilometres, which is similar to the empirical relationships given above and in Wells & Coppersmith (1994) and is a reasonable fit to the earthquakes of M ≥ 6.0 in Fig. 3

The advantage of this approach over some global empirical relationship is that it is more explicit where the assumptions are: A is known to vary regionally (Ekstrom & Dziewonski 1988) and so is d. Moreover, for earthquakes in which the fault length is small compared with the seismogenic thickness, the relationships between moment and magnitude and between moment and fault length are both known to be different from those given above, such that B≈1.0 (Ekstrom and Dziewonski 1988) and M_o is proportional to L³. Thus a single relationship over the whole magnitude range of Fig. 3 (and over the magnitude ranges discussed by Wells & Coppersmith 1994) is not likely to be valid anyway. The explicit approach illustrated here is therefore more likely to be useful for detailed palaeoseismological investigation of specific events.

Estimating Magnitude from an Isoseismal Map - Ambraseys and Jackson (1998)

Ambraseys and Jackson (1998) produced an equation to estimate Surface Magnitude (M_S) from the average radii of isoseismals (r_i) at a specific value of Intensity (I_i).

M_S = −1.54+0.65(I_i)+0.0029(R_i)+2.14 log(R_i)+0.32p (1)

where

R_i =(r_i²+9.7²)^0.5
r, in kilometres, is the mean isoseismal radius of intensity I
p is zero for mean values and one for 84 percentile values (Ambraseys 1992).

Ambraseys and Jackson (1998:395-396) noted that with few exceptions, macroseismic data for the historical period are scanty and the magnitudes that can be calculated from eq. (1) are rather uncertain. They suggested in such cases to use the magnitude estimate to group earthquakes into three broad categories

V, very large events with M. values probably exceeding 8.0
L, large shocks of magnitude between 7.0 and 8.0
M, medium events with M. ranging between 6.0 and 7.0

Pavlides and Caputo (2004) - based on an Aegean dataset

Pavlides and Caputo (2004) examined a dataset of earthquakes from the broader Aegean Region (see Fig. 2 above) and developed a series of empirically based equations to estimate surface magnitude (M_S) of an earthquake from local observations of surface rupture length (SRL), maximum vertical displacement (MVD), and/or average displacement (AD). This resulted in the following regression equations:

M_S = 0.90*log₁₀(SRL) + 5.48          Equation 1

M_S = 0.59*log₁₀(MVD) + 6.75         Equation 2

These equations showed good correlation coefficients (0.84 and 0.82 respectively). Pavlides and Caputo (2004:1) noted that co-seismic fault rupture lengths and especially maximum displacements in the Aegean Region have systematically lower values than the same parameters worldwide, but are similar to those of the Eastern Mediterranean–Middle East region. Pavlides and Caputo (2004) also developed equations to estimate the max and min surface magnitude (M_S) from local observations of surface rupture length (SRL), maximum vertical displacement (MVD), and/or average displacement (AD). These are shown below:

M_Smax = 1.00*log₁₀(SRL) + 5.60          Equation 5

M_Smax = 0.48*log₁₀(MVD) + 7.04         Equation 6

M_Smin = 1.42*log₁₀(SRL) + 4.36          Equation 7

M_Smin = 0.87*log₁₀(MVD) + 6.53         Equation 8

Pavlides and Caputo (2004) also presented equations to solve for surface rupture length (SRL) and maximum vertical displacement (MVD) from surface magnitude (M_S):

log₁₀(SRL) = 0.78*M_S - 3.93          Equation 3

log₁₀(MVD) = 1.14*M_S - 7.82         Equation 4

Figures 5 and 6 (below) show differences between the equations of Wells and Coppersmith (1994), Ambraseys and Jackson (1998), Pavlides and Caputo (2004), and Papazachos and Papazachou (1989).

Calculators

Rupture Lengths and Moment Magnitude from Strike-Slip Fault Displacement - Wells and Coppersmith (1994)

Wells and Coppersmith (1994) - Plots and Tables

from Wells and Coppersmith (1994)
Fig. 11 Regression of average
Fig. 11
1. Regression of average surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 10 Regression of maximum
Fig. 10
1. Regression of maximum surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 13 Surface rupture length
Fig. 13
1. Regression of surface rupture length on average displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on average displacement from Wells and Coppersmith (1994)
Fig. 12 Surface rupture length
Fig. 12
1. Regression of surface rupture length on maximum displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on maximum displacement from Wells and Coppersmith (1994)
Fig. 14 Regression of subsurface
Fig. 14
1. Regression of subsurface rupture length on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture length on magnitude from Wells and Coppersmith (1994)
Table 2A Regressions of Rupture Length,

Table 2A

Regressions of Rupture Length, Rupture Width, Rupture Area, and Moment Magnitude (M)

click on image to open in a new tab

Wells and Coppersmith (1994)

Rupture Width, Rupture Area, and Moment Magnitude from Wells and Coppersmith (1994)
Table 2B Regression of displacement

Table 2B

Regressions of displacement and moment magnitude (M).

click on image to open in a new tab

Wells and Coppersmith (1994)

and moment magnitude from Wells and Coppersmith (1994)
Table 2C Regression of surface

Table 2C

Regressions of surface rupture length and displacement.

click on image to open in a new tab

Wells and Coppersmith (1994)

rupture length and displacement from Wells and Coppersmith (1994)

Variable	Input			Units	Notes
Average Displacement				cm.	Strike-Slip displacement
Maximum Displacement				cm.	Strike-Slip displacement
Variable	Output - not considering a Site Effect			Units	Notes
M_W				unitless	Moment Magnitude for Avg. Displacement (Table 2B, SS)
M_W				unitless	Moment Magnitude for Max. Displacement (Table 2B, SS)
SRL from Avg. Displacement	Direct km	Plotted km		km	Surface Rupture Length, Table 2C SS — hover Direct/Plotted for equations
SRL from Max. Displacement	Direct km	Plotted km		km	Surface Rupture Length, Table 2C SS — hover Direct/Plotted for equations
RLD from Avg. Displacement	Direct1 km	Direct2 km	Plotted km	km	Subsurface Rupture Length, Table 2A SS (via Mw) — hover Direct1/Direct2/Plotted for equations
RLD from Max. Displacement	Direct1 km	Direct2 km	Plotted km	km	Subsurface Rupture Length, Table 2A SS (via Mw) — hover Direct1/Direct2/Plotted for equations

All curves are strike-slip (SS) regressions from Wells and Coppersmith (1994), plotted over a fixed range of 1-1000 cm displacement on a log x-axis; markers overlay the current Average and Maximum Displacement inputs above. Curves/markers are colored by method: Direct1 in blue (RLD plot only), Direct / Direct2 in green, Plotted in purple — solid (SRL plot) or dot (RLD plot) for the Average-Displacement relation, dashed for the Maximum-Displacement relation.
M_W vs. Displacement (Table 2B, SS): M_W = 7.04 + 0.89·log₁₀(Avg. Displacement) and M_W = 6.81 + 0.78·log₁₀(Max. Displacement), displacement in meters.
Surface Rupture Length (SRL): Table 2C provides a genuine second, independently-fit source that skips Mw entirely, so Direct and Plotted are two different lines. Direct (Table 2C's own fit in the needed direction): SRL = 10^{(1.68 + 0.65·log₁₀(Avg. Displacement in m))} km, SRL = 10^{(1.49 + 0.64·log₁₀(Max. Displacement in m))} km. Plotted (algebraic inversion of Table 2C's forward fit, matches Figs. 12/13 exactly): SRL = 10^{(1.6346 + 0.9615·log₁₀(Avg. Displacement in m))} km, SRL = 10^{(1.4569 + 0.8621·log₁₀(Max. Displacement in m))} km — derived by solving log₁₀(AD) = -1.70 + 1.04·log₁₀(SRL) and log₁₀(MD) = -1.69 + 1.16·log₁₀(SRL) (Table 2C SS, the actual "Strike Slip" lines drawn in Figs. 13 and 12) for log₁₀(SRL). These two differ because ordinary least-squares regression is direction-dependent: Table 2C's own SRL-from-displacement row minimizes error in the log(SRL) direction, while its displacement-from-SRL row (used by Plotted) minimizes error in the log(displacement) direction -- two different best-fit lines unless the correlation is perfect.
Subsurface Rupture Length (RLD): Table 2A relates RLD to magnitude, not displacement, so all three answers below still go via Mw (the Mw already computed in the cells above) — there remains no Table 2C-style direct RLD-vs-displacement regression to skip that step entirely. However, Table 2A actually publishes regressions in both directions for the RLD-magnitude relationship (as Table 2B and Table 2C do for their own relationships), so RLD now gets three answers instead of two: Direct1 uses Table 2A's own reverse-direction fit, strike-slip, directly (no inversion): log₁₀(RLD) = -2.57 + 0.62·M_W, i.e. RLD = 10^{(-2.57 + 0.62·M_W)} km. Direct2 is the algebraic inversion of Table 2A's forward fit relating magnitude to RLD (strike-slip): M = 4.33 + 1.49·log₁₀(RLD), which solves to RLD = 10^{(-2.9060 + 0.6711·M_W)} km — this was the only "Direct" answer this calculator gave before Direct1 was added. Plotted reads the same equation as Direct2 off the exact "Strike Slip" line WC94 drew in Fig. 14 (M vs. RLD), so Direct2 and Plotted necessarily coincide and read the same values, exactly as before. Direct1 is the genuinely independent one: because it comes from Table 2A's separate reverse-direction row rather than an inversion of the forward row, it will generally give a different RLD than Direct2/Plotted — mirroring how Table 2C's Direct differs from its Plotted for SRL.
⚠️ Range warning: each output cell now checks its governing input (or, for RLD, the Mw value it depends on) against the exact Magnitude/Displacement/ Rupture-Length Range columns published for the strike-slip rows of Tables 2A, 2B, and 2C. An orange ⚠️ tag appears next to a value whenever the calculation is extrapolating beyond the range of data Wells and Coppersmith actually regressed — hover it for the exact valid range. This is a warning only; it never changes, clamps, or blocks a computed result.

Rupture Lengths and Moment Magnitude from Normal Fault Displacement - Wells and Coppersmith (1994)

Wells and Coppersmith (1994) - Plots and Tables

from Wells and Coppersmith (1994)
Fig. 11 Regression of average
Fig. 11
1. Regression of average surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 10 Regression of maximum
Fig. 10
1. Regression of maximum surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 13 Surface rupture length
Fig. 13
1. Regression of surface rupture length on average displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on average displacement from Wells and Coppersmith (1994)
Fig. 12 Surface rupture length
Fig. 12
1. Regression of surface rupture length on maximum displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on maximum displacement from Wells and Coppersmith (1994)
Fig. 14 Regression of subsurface
Fig. 14
1. Regression of subsurface rupture length on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture length on magnitude from Wells and Coppersmith (1994)
Table 2A Regressions of Rupture Length,

Table 2A

Regressions of Rupture Length, Rupture Width, Rupture Area, and Moment Magnitude (M)

click on image to open in a new tab

Wells and Coppersmith (1994)

Rupture Width, Rupture Area, and Moment Magnitude from Wells and Coppersmith (1994)
Table 2B Regression of displacement

Table 2B

Regressions of displacement and moment magnitude (M).

click on image to open in a new tab

Wells and Coppersmith (1994)

and moment magnitude from Wells and Coppersmith (1994)
Table 2C Regression of surface

Table 2C

Regressions of surface rupture length and displacement.

click on image to open in a new tab

Wells and Coppersmith (1994)

rupture length and displacement from Wells and Coppersmith (1994)

Variable	Input			Units	Notes
Average Displacement				cm.	Normal-Slip displacement
Maximum Displacement				cm.	Normal-Slip displacement
Variable	Output - not considering a Site Effect			Units	Notes
M_W				unitless	Moment Magnitude for Avg. Displacement (Table 2B, N)
M_W				unitless	Moment Magnitude for Max. Displacement (Table 2B, N)
SRL from Avg. Displacement	Direct km	Plotted km		km	Surface Rupture Length, Table 2C N — hover Direct/Plotted for equations
SRL from Max. Displacement	Direct km	Plotted km		km	Surface Rupture Length, Table 2C N — hover Direct/Plotted for equations
RLD from Avg. Displacement	Direct1 km	Direct2 km	Plotted km	km	Subsurface Rupture Length, Table 2A N (via Mw) — hover Direct1/Direct2/Plotted for equations
RLD from Max. Displacement	Direct1 km	Direct2 km	Plotted km	km	Subsurface Rupture Length, Table 2A N (via Mw) — hover Direct1/Direct2/Plotted for equations

All curves are normal-slip (N) regressions from Wells and Coppersmith (1994), plotted over a fixed range of 1-1000 cm displacement on a log x-axis; markers overlay the current Average and Maximum Displacement inputs above. Curves/markers are colored by method: Direct1 in blue (RLD plot only), Direct / Direct2 in green, Plotted in purple — solid (SRL plot) or dot (RLD plot) for the Average-Displacement relation, dashed for the Maximum-Displacement relation.
M_W vs. Displacement (Table 2B, N): M_W = 6.78 + 0.65·log₁₀(Avg. Displacement) and M_W = 6.61 + 0.71·log₁₀(Max. Displacement), displacement in meters. Unlike Reverse, both normal-slip relationships are statistically significant at 95% confidence per Wells and Coppersmith's own t-tests (r = 0.64 and 0.80).
Surface Rupture Length (SRL): Table 2C provides a genuine second, independently-fit source that skips Mw entirely, so Direct and Plotted are two different lines. Direct (Table 2C's own fit in the needed direction): SRL = 10^{(1.52 + 0.28·log₁₀(Avg. Displacement in m))} km, SRL = 10^{(1.36 + 0.35·log₁₀(Max. Displacement in m))} km. Plotted (algebraic inversion of Table 2C's forward fit, matches Figs. 12/13 exactly): SRL = 10^{(1.6048 + 0.8065·log₁₀(Avg. Displacement in m))} km, SRL = 10^{(1.3113 + 0.6623·log₁₀(Max. Displacement in m))} km — derived by solving log₁₀(AD) = -1.99 + 1.24·log₁₀(SRL) and log₁₀(MD) = -1.98 + 1.51·log₁₀(SRL) (Table 2C N, the actual "Normal" lines drawn in Figs. 13 and 12) for log₁₀(SRL). These two differ because ordinary least-squares regression is direction-dependent: Table 2C's own SRL-from-displacement row minimizes error in the log(SRL) direction, while its displacement-from-SRL row (used by Plotted) minimizes error in the log(displacement) direction -- two different best-fit lines unless the correlation is perfect. Both normal-slip Table 2C relationships are statistically significant at 95% confidence (r = 0.59 to 0.73) — unlike Reverse, whose Table 2C relationships WC94 found not significant.
Subsurface Rupture Length (RLD): Table 2A relates RLD to magnitude, not displacement, so all three answers below still go via Mw (the Mw already computed in the cells above) — there remains no Table 2C-style direct RLD-vs-displacement regression to skip that step entirely. However, Table 2A actually publishes regressions in both directions for the RLD-magnitude relationship (as Table 2B and Table 2C do for their own relationships), so RLD now gets three answers instead of two: Direct1 uses Table 2A's own reverse-direction fit, normal, directly (no inversion): log₁₀(RLD) = -1.88 + 0.50·M_W, i.e. RLD = 10^{(-1.88 + 0.50·M_W)} km. Direct2 is the algebraic inversion of Table 2A's forward fit relating magnitude to RLD (normal): M = 4.34 + 1.54·log₁₀(RLD), which solves to RLD = 10^{(-2.8182 + 0.6494·M_W)} km — this was the only "Direct" answer this calculator gave before Direct1 was added. Unlike strike-slip, Fig. 14(b) plots ONLY a strike-slip line for RLD vs. magnitude — no normal-slip curve is drawn there at all, so Plotted cannot be "read off the figure" the way it is for SRL or for SS's RLD. Instead Plotted reuses the same equation as Direct2, and the two coincide — but here that is simply because there is no figure to read a distinct line from, not because the table and figure happen to agree (as for SS). Direct1 remains the genuinely independent one regardless: because it comes from Table 2A's separate reverse-direction row rather than an inversion of the forward row, it will generally give a different RLD than Direct2/Plotted — mirroring how Table 2C's Direct differs from its Plotted for SRL.
⚠️ Range warning: each output cell checks its governing input (or, for RLD, the Mw value it depends on) against the exact Magnitude/Displacement/ Rupture-Length Range columns published for the normal-slip rows of Tables 2A, 2B, and 2C. An orange ⚠️ tag appears next to a value whenever the calculation is extrapolating beyond the range of data Wells and Coppersmith actually regressed — hover it for the exact valid range. This is a warning only; it never changes, clamps, or blocks a computed result.

Rupture Lengths and Moment Magnitude from Reverse Fault Displacement - Wells and Coppersmith (1994)

Wells and Coppersmith (1994) - Plots and Tables

from Wells and Coppersmith (1994)
Fig. 11 Regression of average
Fig. 11
1. Regression of average surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 10 Regression of maximum
Fig. 10
1. Regression of maximum surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 13 Surface rupture length
Fig. 13
1. Regression of surface rupture length on average displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on average displacement from Wells and Coppersmith (1994)
Fig. 12 Surface rupture length
Fig. 12
1. Regression of surface rupture length on maximum displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on maximum displacement from Wells and Coppersmith (1994)
Fig. 14 Regression of subsurface
Fig. 14
1. Regression of subsurface rupture length on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture length on magnitude from Wells and Coppersmith (1994)
Table 2A Regressions of Rupture Length,

Table 2A

Regressions of Rupture Length, Rupture Width, Rupture Area, and Moment Magnitude (M)

click on image to open in a new tab

Wells and Coppersmith (1994)

Rupture Width, Rupture Area, and Moment Magnitude from Wells and Coppersmith (1994)
Table 2B Regression of displacement

Table 2B

Regressions of displacement and moment magnitude (M).

click on image to open in a new tab

Wells and Coppersmith (1994)

and moment magnitude from Wells and Coppersmith (1994)
Table 2C Regression of surface

Table 2C

Regressions of surface rupture length and displacement.

click on image to open in a new tab

Wells and Coppersmith (1994)

rupture length and displacement from Wells and Coppersmith (1994)

⚠︇ Reliability notice: Wells and Coppersmith (1994) tested the reverse-slip-specific relationships used below and found them not statistically significant at 95% confidence — displacement vs. magnitude (r = 0.10 avg, 0.36 max) and SRL vs. displacement (r = 0.28 avg, 0.38 max). In the authors' own words, these relationships are "excluded from further analysis" and "not considered useful for predicting dependent variables," because the regression line is poorly constrained by a small, scattered data set. WC94 recommend using the all-slip-type regression instead when this happens. This calculator shows both below, side by side, so you can compare directly: the R-specific columns are kept for continuity with this site's original calculator and are marked ⚠️ not sig. throughout; the All-slip-type columns are the statistically defensible choice recommended by the paper itself. (Table 2A's reverse-slip Subsurface Rupture Length relationship, r = 0.93, is not affected by this issue and is used as-is.)

Variable	Input		Units	Notes
Average Displacement			cm.	Seismic slip on the ramps
Maximum Displacement			cm.	Seismic slip on the ramps
Variable	Output - not considering a Site Effect				Units	Notes
M_W from Avg. Displacement	R-specific⚠️		All-slip		unitless	Table 2B — hover R-specific/All-slip for equations and significance
M_W from Max. Displacement	R-specific⚠️		All-slip		unitless	Table 2B — hover R-specific/All-slip for equations and significance
SRL from Avg. Displacement	Direct-R⚠️ km	Plotted-R⚠️ km	Direct-All km	Plotted-All km	km	Table 2C — hover Direct/Plotted × R-specific/All-slip for equations
SRL from Max. Displacement	Direct-R⚠️ km	Plotted-R⚠️ km	Direct-All km	Plotted-All km	km	Table 2C — hover Direct/Plotted × R-specific/All-slip for equations
RLD from Avg. Displacement	via R-specific M_W km		via All-slip M_W km		km	Table 2A R (significant, r=0.93), via each M_W source above — Direct = Plotted
RLD from Max. Displacement	via R-specific M_W km		via All-slip M_W km		km	Table 2A R (significant, r=0.93), via each M_W source above — Direct = Plotted

All curves are reverse-slip (R) regressions from Wells and Coppersmith (1994) unless noted, plotted over a fixed range of 1-1000 cm displacement on a log x-axis; markers overlay the current Average and Maximum Displacement inputs above. Curves/markers are colored by source: R-specific in orange (not statistically significant — see banner above), All-slip-type in blue (statistically significant, WC94's recommended fallback).
Moment Magnitude (Table 2B): R-specific: M_W = 6.64 + 0.13·log₁₀(Avg. Displacement) (r = 0.10, NOT significant) and M_W = 6.52 + 0.44·log₁₀(Max. Displacement) (r = 0.36, NOT significant). All-slip-type: M_W = 6.93 + 0.82·log₁₀(Avg. Displacement) (r = 0.75) and M_W = 6.69 + 0.74·log₁₀(Max. Displacement) (r = 0.78), displacement in meters. Wells and Coppersmith explicitly exclude the R-specific rows from further analysis; they are shown here only for continuity with this site's original calculator.
Surface Rupture Length (SRL): Table 2C provides a genuine second, independently-fit source that skips Mw entirely, so Direct and Plotted are two different lines, each available in both R-specific and All-slip flavors. Direct (Table 2C's own fit in the needed direction): R-specific SRL = 10^{(1.45 + 0.26·log₁₀(Avg. Displacement in m))} km (r = 0.28, NOT significant) and SRL = 10^{(1.36 + 0.35·log₁₀(Max. Displacement
in m))} km (r = 0.38, NOT significant); All-slip SRL = 10^{(1.61 + 0.57·log₁₀(Avg. Displacement in m))} km (r = 0.71) and SRL = 10^{(1.43 + 0.56·log₁₀(Max. Displacement in m))} km (r = 0.75). Plotted (algebraic inversion of Table 2C's forward fit): R-specific SRL = 10^{(1.9355 + 3.2258·log₁₀(Avg. Displacement in m))} km and SRL = 10^{(1.0476 + 2.3810·log₁₀(Max. Displacement in m))} km — note how steep and unstable these R-specific inversions are, a direct symptom of the poorly-constrained underlying fit; All-slip SRL = 10^{(1.6250 + 1.1364·log₁₀(Avg. Displacement in
m))} km and SRL = 10^{(1.3529 + 0.9804·log₁₀(Max. Displacement in m))} km. Direct and Plotted differ because ordinary least-squares regression is direction-dependent: the SRL-from-displacement row minimizes error in the log(SRL) direction, while the displacement-from-SRL row (used by Plotted) minimizes error in the log(displacement) direction.
Subsurface Rupture Length (RLD): Wells and Coppersmith published no Table 2C-style direct RLD-vs-displacement regression, so both cells go via Mw, using the algebraic inversion of Table 2A's reverse-slip forward fit relating RLD to magnitude — the one relationship in this panel that is statistically significant (r = 0.93): M = 4.49 + 1.49·log₁₀(RLD), which solves to RLD = 10^{(-3.0134 + 0.6711·M_W)} km. As with Normal-slip, Fig. 14(b) plots ONLY a strike-slip line for RLD vs. magnitude — no reverse-slip curve is drawn there at all, so Plotted cannot be "read off the figure." Instead Direct and Plotted both use the same Table 2A reverse-slip forward fit, algebraically inverted, applied once for each of the two Mw sources above (R-specific and All-slip).
⚠️ Range warning (orange): each output cell checks its governing input (or, for RLD, the Mw value it depends on) against the exact Magnitude/Displacement/ Rupture-Length Range columns published for the relevant rows of Tables 2A, 2B, and 2C. An orange ⚠️ tag appears next to a value whenever the calculation is extrapolating beyond the range of data Wells and Coppersmith actually regressed — hover it for the exact valid range. This is a warning only; it never changes, clamps, or blocks a computed result.
⚠️ Not-significant marker (red): a separate, persistent red tag marks every R-specific Mw and SRL value, regardless of range, because Wells and Coppersmith found these particular regressions statistically unreliable at any input value — see the banner at the top of this panel for the full explanation.

Moment Magnitude from Strike-Slip Fault Surface Rupture Length - Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Rupture Length		km.	Rupture Length
Variable	Output - not considering a Site Effect	Units	Notes
M_W		unitless	Moment Magnitude

Curve shows M_W = 5.16 + 1.12·log₁₀(Rupture Length), Rupture Length in km (Wells and Coppersmith, 1994), plotted over a fixed range of 1-1000 km on a log x-axis. The Plot button also overlays the current Rupture Length input above as a marker.

Moment Magnitude from Normal Fault Surface Rupture Length - Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Rupture Length		km.	Rupture Length
Variable	Output - not considering a Site Effect	Units	Notes
M_W		unitless	Moment Magnitude

Curve shows M_W = 4.86 + 1.32·log₁₀(Rupture Length), Rupture Length in km (Wells and Coppersmith, 1994), plotted over a fixed range of 1-1000 km on a log x-axis. The Plot button also overlays the current Rupture Length input above as a marker.

Moment Magnitude from Reverse Fault Surface Rupture Length - Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Rupture Length		km.	Fault Break
Variable	Output - not considering a Site Effect	Units	Notes
M_W		unitless	Moment Magnitude

Curve shows M_W = 5.0 + 1.22·log₁₀(Rupture Length), Rupture Length in km (Wells and Coppersmith, 1994), plotted over a fixed range of 1-1000 km on a log x-axis. The Plot button also overlays the current Rupture Length input above as a marker.

Wells and Coppersmith (1994) - Plots and Tables

Fig. 9 Regression of surface
Fig. 9
1. Regression of surface rupture length on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture length on magnitude from Wells and Coppersmith (1994)
Fig. 10 Regression of maximum
Fig. 10
1. Regression of maximum surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 11 Regression of average
Fig. 11
1. Regression of average surface displacement on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
surface displacement on magnitude from Wells and Coppersmith (1994)
Fig. 12 Surface rupture length
Fig. 12
1. Regression of surface rupture length on maximum displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on maximum displacement from Wells and Coppersmith (1994)
Fig. 13 Surface rupture length
Fig. 13
1. Regression of surface rupture length on average displacement. Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
on average displacement from Wells and Coppersmith (1994)
Fig. 14 Regression of subsurface
Fig. 14
1. Regression of subsurface rupture length on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture length on magnitude from Wells and Coppersmith (1994)
Fig. 15 Regression of downdip
Fig. 15
1. Regression of downdip rupture width on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
rupture width on magnitude from Wells and Coppersmith (1994)
Fig. 16 Regression of rupture
Fig. 16
1. Regression of rupture area on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval.
2. Regression lines for strike-slip, reverse, and normal-slip relationships.
See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)
area on magnitude from Wells and Coppersmith (1994)
Fig. 17 Stable continental
Fig. 17

Regression lines for stable continental region (SCR) earthquakes and non-SCR continental earthquakes.
1. Regression of subsurface rupture length on magnitude (M).
2. Regression of rupture area on magnitude (M).
click on image to open in a new tab

Wells and Coppersmith (1994)
region and non-SCR regressions from Wells and Coppersmith (1994)
Table 2A Regressions of Rupture Length,

Table 2A

Regressions of Rupture Length, Rupture Width, Rupture Area, and Moment Magnitude (M)

click on image to open in a new tab

Wells and Coppersmith (1994)

Rupture Width, Rupture Area, and Moment Magnitude from Wells and Coppersmith (1994)
Table 2B Regression of displacement

Table 2B

Regressions of displacement and moment magnitude (M).

click on image to open in a new tab

Wells and Coppersmith (1994)

and moment magnitude from Wells and Coppersmith (1994)
Table 2C Regression of surface

Table 2C

Regressions of surface rupture length and displacement.

click on image to open in a new tab

Wells and Coppersmith (1994)

rupture length and displacement from Wells and Coppersmith (1994)

Moment or Surface Magnitude from Rupture Length - not Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Rupture Length		km.	Rupture Length
Variable	Output - not considering a Site Effect	Units	Notes	Plot
M_W		unitless	Moment Magnitude from Ambraseys (1988) (developed for the Middle East)
M_W		unitless	Moment Magnitude from Bonilla and Lienkaemper (1984)
M_S		unitless	Surface Magnitude from Ambraseys and Jackson (1998) Eqn. 2
M_S		unitless	Surface Magnitude from Ambraseys and Jackson (1998) Eqn. 3
M_W		unitless	Moment Magnitude from Ambraseys and Jackson (1998) Eqn. 11
M_S		unitless	Avg. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 1 (developed for the Aegean)
M_Smin		unitless	Min. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 7 (developed for the Aegean)
M_Smax		unitless	Max. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 5 (developed for the Aegean)

Moment or Surface Magnitude from Maximum Vertical Displacement - not Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Max. Vertical Displacement		m	Max. Vertical Displacement
Variable	Output - not considering a Site Effect	Units	Notes	Plot
M_S		unitless	Avg. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 2 (developed for the Aegean)
M_Smin		unitless	Min. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 2 (developed for the Aegean)
M_Smax		unitless	Max. Surface Magnitude from Pavlides and Caputo (2004) Eqn. 2 (developed for the Aegean)

Estimating Magnitude from an Isoseismal Map

Estimate Surface Magnitude (M_S) from Avg. radii of isoseismals (r_i) at a specific value of Intensity (I_i)
Source - Ambraseys and Jackson (1998)

Variable	Input	Units	Variable Name
r_i		km.	Mean isoseismal radius for a given Intensity I
I_i		unitless	The given Intensity
p		unitless	p=0 for mean values. p=1 for 84 percentile values (Ambraseys, 1992)
Variable	Output	Units	Notes
M_S		unitless	Surface Magnitude

Moment Magnitude from Fault Length and Width

Fig. 16 Regression of rupture area

Fig. 16

Regression of rupture area on magnitude (M). Regression line shown for all-slip-type relationship. Short dashed line indicates 95% confidence interval. Regression lines for strike-slip, reverse, and normal-slip relationships. See Table 2 for regression coefficients. Length of regression lines shows the range of data for each relationship.

click on image to open in a new tab

Wells and Coppersmith (1994)

on magnitude from Wells and Coppersmith (1994)

Variable	Input	Units	Notes
Fault Length		km.
Fault Width		km.
Variable	Output	Units	Notes
M_w		unitless	Moment Magnitude computed using Wesnousky (2008)
M_w		unitless	Moment Magnitude computed using Hanks and Bakun (2008)
Fault Area		km.²

Plots

not fully QCed but appears to be largely OK when compared to Fig. 5 and 6 of Pavlides and Caputo (2004)

Magnitude (M) vs. Surface Rupture Length (SRL)

Magnitude (M) vs. Maximum Vertical Displacement (MVD)

References

Anderson, J., et al. (2021). "Improved Scaling Relationships for Seismic Moment and Average Slip of Strike-Slip Earthquakes Incorporating Fault-Slip Rate, Fault Width, and Stress Drop." Bulletin of the Seismological Society of America 111.

Ambraseys, N. (1988). "Magnitude-fault length relationships for earthquakes in the Middle East," in Lee, W. H. (ed.), History of Seismograms and Earthquakes of the World, Academic, San Diego, Calif., 309-310.

Ambraseys, N. (1992). Soil mechanics and engineering seismology. Invited Lecture, Proceedings of the 2nd National Conference on Geotechnical Engineering, Thessaloniki, pp. xxi-xlii.

Ambraseys, N. N., and Jackson, J. A. (1998). "Faulting associated with historical and recent earthquakes in the Eastern Mediterranean region." Geophysical Journal International 133(2): 390-406.

Bonilla, M., and Lienkaemper (1984). In: Bullen, K. E., and Bolt, B. A. (1993). An Introduction to the Theory of Seismology, 4th ed., Cambridge.

Darawcheh, R., et al. (2000). "The 9 July 551 AD Beirut earthquake, Eastern Mediterranean region." Journal of Earthquake Engineering 4(4): 403-414.

Hanks, T. C., and Bakun, W. H. (2008). "M-log A observations for recent large earthquakes." Bulletin of the Seismological Society of America 98(1): 490-494.

Pavlides, S., and Caputo, R. (2004). "Magnitude versus faults' surface parameters: quantitative relationships from the Aegean Region." Tectonophysics 380(3): 159-188.

Wells, D. L., and Coppersmith, K. J. (1994). "New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement." Bulletin of the Seismological Society of America 84(4): 974-1002.

Wesnousky, S. (2008). "Displacement and Geometrical Characteristics of Earthquake Surface Ruptures: Issues and Implications for Seismic-Hazard Analysis and the Process of Earthquake Rupture." Bulletin of the Seismological Society of America 98.

Explanation

Open Explanations in a new tab

SEISMERIO

Open SEISMERIO in a new tab

References

Bentley, J.L. and Ottmann, T. (1979). "Algorithms for Reporting and Counting Geometric Intersections." IEEE Transactions on Computers C-28(9), 643-647.

Cinti, F.R., Pantosti, D., Lombardi, A.M. and Civico, R. (2021). "Modeling of Earthquake Chronology from Paleoseismic Data: Insights for Regional Earthquake Recurrence and Earthquake Storms in the Central Apennines." Tectonophysics 816, 229016.

Lombardi, A.M., Cinti, F.R. and Pantosti, D. (2025). "Paleoearthquakes Modelling and Effects of Uncertainties on Probability Assessment of Next Fault Ruptures: The Case of Central Italy Surface Faulting Earthquakes." Geophysical Journal International 241(2), 1327-1347.

Lombardi, A.M., Cinti, F.R. and Pantosti, D. (2026). "POPE: A Software Package for a Reliable Reconstruction of Paleoseismicity." Earth Science Informatics 19, 94.

Explanation

V_S30 Site Effect Explanation

The value given for Intensity with site effect removed is how much you should subtract from your Intensity estimate to obtain a pre-amplification value for Intensity. For example if the output is 0.5 and you estimated an Intensity of 8, your pre-amplification Intensity is now 7.5. An Intensity estimate with the site effect removed is helpful in producing an Intensity Map that will do a better job of "triangulating" the epicentral area. If you enter a V_S30 greater than 655 m/s you will get a positive number, indicating that the site amplifies seismic energy. If you enter a V_S30 less than 655 m/s you will get a negative number, indicating that the site attenuates seismic energy rather than amplifying it. Intensity Reduction (I_reduction) is calculated based on Equation 6 from Darvasi and Agnon (2019).

V_S30 Explanation

V_S30 is the average seismic shear-wave velocity from the surface to a depth of 30 meters at earthquake frequencies (below ~5 Hz.). Darvasi and Agnon (2019) estimated V_S30 for a number of sites in Israel. If you get V_S30 from a well log, you will need to correct for intrinsic dispersion. There is a seperate geometric dispersion correction usually applied when processing the waveforms however geometric dispersion corrections are typically applied to a borehole Flexural mode generated from a Dipole source and for Dipole sources propagating in the first 30 meters of soft sediments, modal composition is typically dominated by the Stoneley wave. Shear from Stoneley estimates are approximate at best. This is a subject not well understood and widely ignored by the Geotechnical community and/or Civil Engineers but understood by a few specialists in borehole acoustics. Other considerations will apply if you get V_S30 value from a cross well survey or a shallow seismic survey where the primary consideration is converting shear slowness from survey frequency to Earthquake frequency. There are also ways to estimate shear slowness from SPT & CPT tests.

Calculator - Intensity Reduction due to V_S30 Site Effect

Source - Darvasi, Y. and A. Agnon (2019)

Variable	Input	Units	Notes
V_S30		m/s	Enter a value of 655 for no site effect Equation comes from Darvasi and Agnon (2019)
Variable	Output - Site Effect Removal	Units	Notes
I_reduction		unitless	Reduce Intensity Estimate by this amount to get a pre-amplification value of Intensity

References

Darvasi, Y., and Agnon, A. (2019). "Calibrating a new attenuation curve for the Dead Sea region using surface wave dispersion surveys in sites damaged by the 1927 Jericho earthquake." Solid Earth 10(2): 379-390.

Papers at the Geophysical Institute of Israel related to site effect - recommended by Amos Salamon, who noted that microzonation site effect maps have been created for cities in Israel

Zaslavsky, Y., Shapira, A., Gorstein, M., Perelman, N., Ataev, G., and Aksinenko, T. (2012). "Questioning the applicability of soil amplification factors as defined by NEHRP (USA) in the Israel building standards." Natural Science 4: 631-639.

Explanation

Salamon et. al. (2010) noted that seismic amplification could occur on slopes greater than 60 degrees where the slope height is roughly equal to one fifth of a seismic wavelength. Turning this relationship around, the frequency at which this effect will occur is defined as follows :

f = V_S/(5*H)

where
f = frequency (Hz.)
V_S = Shear Wave Velocity (m/s)
H = slope height in meters

Amos Salamon (personal communication, 2024) cautions that this equation was an ad hoc procedure used for his report on Jerusalem (Salamon et al., 2010) and its extrapolation to other sites without site specific investigations is not recommended. That said, I saw a similar equation in the past but cannot remember the citation.

Calculator and Plot

Source - Salamon et. al. (2010)

**Slope Effect Calculator**
Variable	Input	Units	Notes
V_S		m/s	Shear Wave Velocity
H		m	Slope Height
Variable	Output	Units	Notes
f		Hz.	Frequency

Plot

References

Salamon, A., et al. (2010). "Zones of required investigation for earthquake-related hazards in Jerusalem." Natural Hazards 53(2): 375-406.

Explanation

Figure 13a from Massa et al (2010)

Figure 13. (a)

Residuals between predicted acceleration response spectra (5% damping) for reference station (NRN2) and for station NRN7, for periods up to 1 s. The results are reported for the west—east component and are presented in terms of logarithmic differences. PGHA indicates peak ground horizontal component (in this case, the east—west component).

Massa et al (2010)

Output with site effect removed assumes that PGA is higher than it would be if there was no site effect. In this situation, Intensity (I) with site effect removed is calculated pre-amplification (i.e. it will be lower). This is because an Intensity estimate with the site effect removed is helpful in producing an Intensity Map that will do a better job of "triangulating" the epicentral area.

Site Effect is based on Equation 2 and Figure 13 a of

Massa et al (2010). In their study, they estimated a frequency dependent additional PGA (St in Eqn. 2) which is added by a topographic site effect. The additional topographic site effect PGA varied from ~0.1 g to 0.5 g for dominant frequencies of approximately 1 - 5 Hz.. Higher PGA's were shown to be present for higher frequencies which are more likely to occur when the earthquake producing fault is closer to the site. They also noted that a greater topographic effect was observed when the seismic energy arrived orthogonal (perpendicular in their words) to the ridge. The additional Site Effect PGA is linearly scaled from 0 - 0.5 g for site effects where amplitude increases from 1x to 10x. It's not the greatest transform to remove site effect from the Intensity estimate but may be useful for crude estimates.

Calculator - Estimate Magnitude and Intensity with and without a Site (Ridge) Effect

Sources
- Conversion from PGA to Intensity using Wald et al (1999)
- Magnitude is calculated from Intensity (I) and Fault Distance (R) based on Hough and Avni (2009) who did not specify the type of Magnitude scale they were using.

Variable	Input	Units	Notes
PGA		g	Peak Horizontal Ground Acceleration
R		km.	Distance to earthquake producing fault
Seismic Amplification		unitless	Site Effect due to Topographic or Ridge Effect (set to 1 to assume no site effect)
Variable	Output - Site Effect not considered	Units	Notes
I		unitless	Conversion from PGA to Intensity using Wald et al (1999)
M		unitless	Attenuation relationship of Hough and Avni (2009) used to calculate Magnitude
Variable	Output - Site Effect removed	Units	Notes
I		unitless	Conversion from PGA to Intensity using Wald et al (1999)
M		unitless	Attenuation relationship of Hough and Avni (2009) used to calculate Magnitude

References

Hough, S. E., and Avni, R. (2009). "The 1170 and 1202 Dead Sea Rift earthquakes and long-term magnitude distribution on the Dead Sea fault zone." Israel Journal of Earth Sciences 58(3-4): 295-308.

Massa, M., et al. (2010). "An experimental approach for estimating seismic amplification effects at the top of a ridge, and the implication for ground-motion predictions: the case of Narni, central Italy." Bulletin of the Seismological Society of America 100(6): 3020-3034.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Explanations

How the Strike-Normal / Average Horizontal Ratio Calculator Works

This calculator implements part of the rupture directivity model of Somerville et al. (1997), published in Seismological Research Letters. The model describes how the strike-normal component of horizontal ground motion compares to the average horizontal motion otherwise predicted by an attenuation relation, as a function of magnitude and distance from the fault.

The ratio is fit using the equation y = C1 + C2 ln(r_rup + 1) + C3(M - 6), for M greater than 6, where r_rup is the closest distance to the fault in kilometres and M is moment magnitude. C1, C2, and C3 are period-dependent coefficients taken from Table 6 of Somerville et al. (1997). This version of the model excludes dependence on the azimuth angle θ (strike-slip) or zenith angle φ (dip-slip). Somerville et al. (1997) also present an angle-dependent version, in Table 7, modulated by cos 2ξ, which is not implemented in this calculator. Somerville et al. (1997) found that the effects of the length and width ratios X and Y, site category, and faulting mechanism on this ratio were not significant, and dropped them from the model.

The strike-normal to average ratio is calculated as the exponential of y. Somerville et al. (1997) state that the strike-normal motion is obtained by multiplying the attenuation relation value by this ratio, and the strike-parallel motion is obtained by dividing the attenuation relation value by the same ratio. The calculator reports both the strike-normal ratio and its reciprocal. The "ratio vs period" plot fixes magnitude and shows the ratio across the periods tabulated in Table 6, for a set of distances, reproducing the form of the upper panels of Figure 13 in Somerville et al. (1997). The "ratio vs distance" plot fixes period and shows the ratio across a continuous range of distance, for magnitudes 6.0, 6.5, 7.0, and 7.5, reproducing the form of the lower panels of Figure 13 in Somerville et al. (1997). Somerville et al. (1997) tabulate coefficients for this ratio at magnitudes down to 6.0, and for closest distances of 0-50 km. Coefficients are only given for the periods listed in Table 6, between 0.5 and 6.0 seconds; the calculator does not interpolate beyond these tabulated periods.

Calculators

Strike-Normal / Average Horizontal Ratio Calculator for Strike Slip Faults

Fig. 2 Schematic map view

Fig. 2

Schematic map view of the radiation pattern for a vertical strike-slip fault and its effect on near-fault ground displacements.

Click on image to open in a new tab.

Somerville et al. (1997)>

of the radiation pattern for a vertical strike-slip fault and its effect on near-fault ground displacements from Somerville et al. (1997)
Fig. 13 Empirical model

Fig. 13

Empirical model of the strike-normal to average horizontal response spectral ratio excluding dependence on the angles θ or φ, shown as a function of period for various magnitudes and distances (top), and as function of distance for various magnitudes and periods (bottom).

Click on image to open in a new tab.

Somerville et al. (1997)>

of the strike-normal to average horizontal response spectral ratio, showing its dependence on period and distance from Somerville et al. (1997)
Fig. 17 Schematic diagram

Fig. 17

Schematic diagram of the polarity of permanent ground displacement for strike-slip earthquakes. The motions are shown for both left-lateral and right-lateral unilateral faults, and for both northerly and southerly rupture propagation on north-striking faults.

Click on image to open in a new tab.

Somerville et al. (1997)>

of the polarity of permanent ground displacement for strike-slip earthquakes from Somerville et al. (1997)

Single-value calculator

Variable	Input	Units	Notes
Magnitude (M)		Mw	Model valid for M > 6
Rupture Distance (r_rup)		km	Model tabulated for r_rup 0-50 km
Period		sec	Restricted to periods tabulated in Table 6
Variable	Output	Units	Notes
FN/Average Ratio (Strike-Normal / Average)		ratio	Multiplier applied to average horizontal motion for strike-normal component
Strike-Parallel / Average		ratio	Reciprocal of the strike-normal ratio

Ratio vs period (fixed magnitude, several distances)

Magnitude (M)

FN/Average Ratio is the strike-normal component of horizontal ground motion divided by the average horizontal motion predicted by an attenuation relation (Somerville et al. 1997). r_rup is the closest distance from the site to the fault rupture, in km.

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Period

FN/Average Ratio is the strike-normal component of horizontal ground motion divided by the average horizontal motion predicted by an attenuation relation (Somerville et al. 1997). r_rup is the closest distance from the site to the fault rupture, in km.

Strike-Normal / Average Horizontal Ratio Calculator for Dip Slip Faults

Fig. 9 Empirical model

Fig. 9

Empirical model of the response spectral amplitude ratio, showing its dependence on period and on the directivity function (Xcos θ for strike-slip; Ycos φ for dip-slip).

Click on image to open in a new tab.

Somerville et al. (1997)>

of the response spectral amplitude ratio, showing its dependence on period and directivity function from Somerville et al. (1997)

Single-value calculator

Variable	Input	Units	Notes
Magnitude (M)		Mw	Model valid for M > 6
Rupture Distance (r_rup)		km	Model tabulated for r_rup 0-50 km
Period		sec	Restricted to periods tabulated in Table 6
Variable	Output	Units	Notes
FN/Average Ratio (Strike-Normal / Average)		ratio	Multiplier applied to average horizontal motion for strike-normal component
Strike-Parallel / Average		ratio	Reciprocal of the strike-normal ratio

Ratio vs period (fixed magnitude, several distances)

Magnitude (M)

FN/Average Ratio is the strike-normal component of horizontal ground motion divided by the average horizontal motion predicted by an attenuation relation (Somerville et al. 1997). r_rup is the closest distance from the site to the fault rupture, in km. This model does not distinguish between strike-slip and dip-slip mechanisms.

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Period

FN/Average Ratio is the strike-normal component of horizontal ground motion divided by the average horizontal motion predicted by an attenuation relation (Somerville et al. 1997). r_rup is the closest distance from the site to the fault rupture, in km. This model does not distinguish between strike-slip and dip-slip mechanisms.

References

Somerville, P. G., Smith, N. F., Graves, R. W., and Abrahamson, N. A. (1997). "Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity." Seismological Research Letters 68(1): 199–222.

Explanation

Rodkin and Korzhenkov (2018) presented two ways to estimate Peak Ground Velocity (PGV) - the Tilt Method (my name) and the PGV estimation method (PGVEM - their name).

Tilt Method

Fig. 11 from Rodkin and Korzhenkov (2018) -
Fig. 11

A sketch map showing the destruction of
1. an ideal rigid wall
2. a more realistic wall composed of blocks of stones separated by joints
Rodkin and Korzhenkov (2018)
Figure 4 from Korzhenkov and Mazor (2014) -

Fig. 4

A tilt southward of the southern wall at the SE premises of the Northern Church (field station 3). The degree of the tilting is increasing with the distance from the abutted perpendicular wall. This phenomenon is the result of maximum freedom of oscillation at the central part of the wall

Korzhenkov and Mazor (2014)

This method requires as input the Critical Tilt angle (α) of a wall in order for it to collapse. If the tilt is large enough, the projection of the wall's center of gravity will be located outside its base (see Fig. 11) and the wall will fall over. In order to estimate the Critical Tilt angle (α), we need to come up with some wall dimensions and input them into the calculator below. Calculated critical tilt angle is for a rigid wall. If the wall is composed of blocks which are mortared together, as the seismic forces cause the wall to tilt the top of the wall may start to bend and fail. If the top of the wall is destructed, the lower part of the wall will have a different effective geometry and require a larger tilt to fall over. Archaeoseismic observations can help produce a realistic tilt angle. For example, Rodkin and Korzhenkov (2018) noted that tilt angles in the lower parts of walls in Rehovot ba-Negev reached 15° to 20° (e.g. see Figure 4) while critical title angle based on geometry of the site and the calculator below leads to a values of 11°-12°. In this case, the larger observed angles are preferred.

Structure	Height (m)	Thickness (m)	α - Critical Tilt Angle
Church
House

PGV Estimation Method

Fig. 13 from Korzhenkov and Mazor (2014) -

Fig. 13

A horizontal 15 cm shift eastward of the upper part of an arch column in one of the excavated quarters

Korzhenkov and Mazor (2014)
Figure 16 from Korzhenkov and Mazor (2014) -

Fig. 16

Clockwise rotation of a stone in an eastern wall (field station 9)

Korzhenkov and Mazor (2014)

The PGV Estimation Method also requires two inputs - the coefficient of friction (k) of the sliding masonry block and the observed displacement of the block. At Rehovot ba-Negev, Rodkin and Korzhenkov (2018) estimated that k varied from 0.8 - 1.0 and displacement went as high as 10 - 15 cm. (the larger values are more important in their method). An example of the larger observed shift of ~15 cm. at Rehovot ba-Negev can be seen in Figure of 13 of Korzhenkov and Mazor (2014). Another example can be seen in Figure 16 from the same article. Although the PGV Estimation Method is their preferred method, there were apparently a limited number of displacement measurements in Rehovot ba-Negev. Thus, they included the Tilt method to help constrain reasonable PGV values. Inputting their suggested range of k values and displacement values leads to PGV values between 1.3 and 1.7 m/s - higher than what one obtains with the Tilt Method.

Calculators

Tilt Method Calculator

Source - Rodkin and Korzhenkov (2018)
Conversion from PGV to Intensity is made using Equation 2 of Wald et al (1999) (only valid for I between V and IX).

Variable	Input	Units	Notes
α		degrees	Critical Tilt Angle
H		m	Wall Thickness
Variable	Output - not considering a Site Effect	Units	Notes
PGV		m/s	Peak Ground Velocity
I		unitless	Intensity

PGV Estimation Method Calculator

Source - Rodkin and Korzhenkov (2018)
Conversion from PGV to Intensity is made using Equation 2 of Wald et al (1999) (only valid for I between V and IX).

Variable	Input	Units	Notes
k		unitless	Coefficient of friction
Displacement		cm.	Displacement of masonry
Variable	Output - not considering a Site Effect	Units	Notes
PGV		m/s	Peak Ground Velocity
I		unitless	Intensity

References

Korzhenkov, A. M., and Mazor, E. (2014). "Archaeoseismological damage patterns at the ancient ruins at Rehovot-ba-Negev, Israel." Archaeologischer Anzeiger: 75-92.

Rodkin, M. V., and Korzhenkov, A. M. (2018). "Estimation of maximum mass velocity from macroseismic data: A new method and application to archeoseismological data." Geodesy and Geodynamics.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Explanation

2D Model used by Wechsler et al (2009) for Umm Qanatir

Static Analysis

A Factor of Safety (FS) for the slope is estimated first to determine if the slope was stable under aseismic conditions. Two methods are considered here - the Fellenius method and the modified Bishop method. Both methods divide the soil model into vertical slices and determine Factor of Safety as a ratio from a sum of moment balances performed on each vertical slice. This accounts for changes in topography and lateral changes in unit thicknesses and elevation of the water table. The generalized equation is shown below.

FS = Σ M_r / Σ M_d

where

M_r = Resisting Moment
M_d = Driving Moment

Resisting Moment is the ability of the soil mass to avoid moving. The driving moment is the forces such as gravity and water saturated layers pushing the soil mass down slope. FS less than 1 indicates that the slope is unstable. FS greater than 1 indicates that the slope is stable. Factor of Safety tends to be sensitive to the height of the water table. Lower values of FS are associated with shallower water tables. If you know the time of year an earthquake struck, this could help you estimate the height of the water table. Well data can also be helpful. Ideally, mechanical tests on soil layers can inform your 2 model of the various layers. Wechsler et al (2009) used the commercial software Slope/W™ to perform the Static Analysis at Umm Qanatir.

Dynamic Analysis

The Newmark Displacement method can be used to evaluate slope stability during an earthquake. First a critical acceleration is estimated. Critical acceleration is the minimum earthquake induced acceleration that initiates slope movement. Critical acceleration is computed as follows:

a_c = (FS-1)sinβ

where

a_c = critical acceleration measured in g's (1 g = 9.81 m/s²)
FS = Factor of Safety (computed previously for a range of conditions)
β = Thrust angle (degrees)

Thrust Angle

Newmark (1965)'s slope stability model

Fig. 15 a

O = Circle center
c.g. = Center of Gravity
β = Thrust angle

Newmark (1965)

showing thrust angle (β)

For a planar slide, thrust angle (β) is the direction the COG of the sliding block moves when displacement initially occurs. Ideally this is the dip of the bedding plane. In regional studies this is typically approximated by the slope angle (Katz and Crouvi, 2007 citing Miles and Keefer, 2001). For rotational movement on a circular surface, Newmark (1965) showed that the thrust angle is the angle between the vertical and a line segment connecting the center of gravity of the landslide mass and the center of the slip circle ( Jibson, 1996:310).

If strong motion records from the area are lacking, the Newmark displacement D_N can be estimated using an empirically derived formula from data from Southern California. The empirical relationship comes from Jibson et al (2000: p. 8 eqn. 3) which estimates the critical displacement D_N at which the slope begins to fail.

lnD_N = 1.521*ln(I_α) - 1.993ln(a_c) - 1.546

where

D_N = Newmark Displacement (cm.)
I_α = Arias Intensity (m/s)
a_c = Critical acceleration (g's)

Arias Intensity (I_α) can be related to Magnitude and Fault Distance using an equation derived for the Dead Sea by Katz and Crouvi (2007):

log₁₀I_α = 1.2M_W - 2.2log₁₀R - 4.9

where

I_α = Arias Intensity
M_W = Moment Magnitude
R = Fault Distance (km.)

By assuming a D_N of 5 or 10 cm., one can solve for I_α and then M_W as a function of R.

Ridge Site Effect Removal Methodology

Figure 13a from Massa et al (2010)

Figure 13. (a) Residuals between predicted acceleration response spectra (5% damping) for reference station (NRN2) and for station NRN7, for periods up to 1 s. The results are reported for the west—east component and are presented in terms of logarithmic differences. PGHA indicates peak ground horizontal component (in this case, the east—west component).

Massa et al (2010)

Output with site effect removed assumes that PGA is higher than it would be if there was no site effect. In this situation, Intensity (I) with site effect removed is calculated pre-amplification (i.e. it will be lower). This is because an Intensity estimate with the site effect removed is helpful in producing an Intensity Map that will do a better job of "triangulating" the epicentral area.

Site Effect is based on Equation 2 and Figure 13 a of

Massa et al (2010). In their study, they estimated a frequency dependent additional PGA (St in Eqn. 2) which is added by a topographic site effect. The additional topographic site effect PGA varied from ~0.1 g to 0.5 g for dominant frequencies of approximately 1 - 5 Hz.. Higher PGA's were shown to be present for higher frequencies which are more likely to occur when the earthquake producing fault is closer to the site. They also noted that a greater topographic effect was observed when the seismic energy arrived orthogonal (perpendicular in their words) to the ridge. Both of these considerations suggest that a topographic ridge effect should be considered when other evidence suggests that a nearby fault broke during the earthquake. The additional Site Effect PGA is linearly scaled from 0 - 0.5 g for site effects where amplitude increases from 1x to 10x. It's not the greatest transform to remove site effect from the Intensity estimate but may be useful for crude estimates.

Calculators

2D Model used by Wechsler et al (2009)

Variable	Input	Units	Notes
FS		unitless
β		degrees
D_N		cm.	Wechsler et al (2009) recommends a value of 5 or 10
R		km.	Distance to nearest earthquake producing fault
Variable	Output (No Site Effect)	Units	Notes
a_c		g	minimum acceleration to induce slide
I		unitless	Conversion from a_c to I using Wald et al (1999)
M		unitless	Attenuation relationship of Hough and Avni (2009) used to calculate Magnitude from I and R
I_α		m/s	Calculated from eqn. 2 of Wechsler et al (2009)
I_α		m/s	Calculated from eqn. 3.17 of (Kramer, 1996:87)
M_w		unitless	calculated from eqn. 3 of Wechsler et al (2009) which comes from Katz and Crouvi (2007)
Variable	Input	Units	Notes
Seismic Amplification		unitless	Site Effect due to Topographic or Ridge Effect (set to 1 to assume no site effect)
Variable	Output (Site Effect)	Units	Notes
I		unitless	Intensity with Topographic Effect removed
M		unitless	Magnitude with Topographic Effect removed - using Hough and Avni (2009)
M_W		unitless	Moment Magnitude with Topographic Effect removed M_W from eqn. 3 of Wechsler et al (2009) which comes from Katz and Crouvi (2007)

CAVEAT

References

Hough, S. E., and Avni, R. (2009). "The 1170 and 1202 Dead Sea Rift earthquakes and long-term magnitude distribution on the Dead Sea fault zone." Israel Journal of Earth Sciences 58(3-4): 295-308.

Jibson, R. W. (1996). "Use of landslides for paleoseismic analysis." Engineering Geology 43(4): 291-323.

Jibson, R. W., et al. (2000). "A method for producing digital probabilistic seismic landslide hazard maps." Engineering Geology 58(3): 271-289.

Katz, O., and Crouvi, O. (2007). "The geotechnical effects of long human habitation (Less Than 2000 years): Earthquake-induced landslide hazard in the city of Zefat, northern Israel." Engineering Geology 95(3-4): 57-78.

Massa, M., et al. (2010). "An experimental approach for estimating seismic amplification effects at the top of a ridge, and the implication for ground-motion predictions: the case of Narni, central Italy." Bulletin of the Seismological Society of America 100(6): 3020-3034.

Miles, S., and Keefer, D. K. (2001). Seismic Landslide Hazard for the City of Berkeley, California. USGS Miscellaneous Field Studies Map 2378.

Newmark, N. M. (1965). "Effects of earthquakes on dams and embankments." Géotechnique 15(2): 139-160.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Wechsler, N., et al. (2009). "Estimating location and size of historical earthquake by combining archaeology and geology in Umm-El-Qanatir, Dead Sea Transform." Natural Hazards 50(1): 27-43.

Explanation

Salamon and Di Manna Plot

Salamon and Di Manna (2019) created a bounding envelope for landslide tsunamis based on a curated data set.

Calculators and Plotters

Salamon and Di Manna Plot

Bounding Envelopes for landslide tsunamis from Salamon and Di Manna (2019)

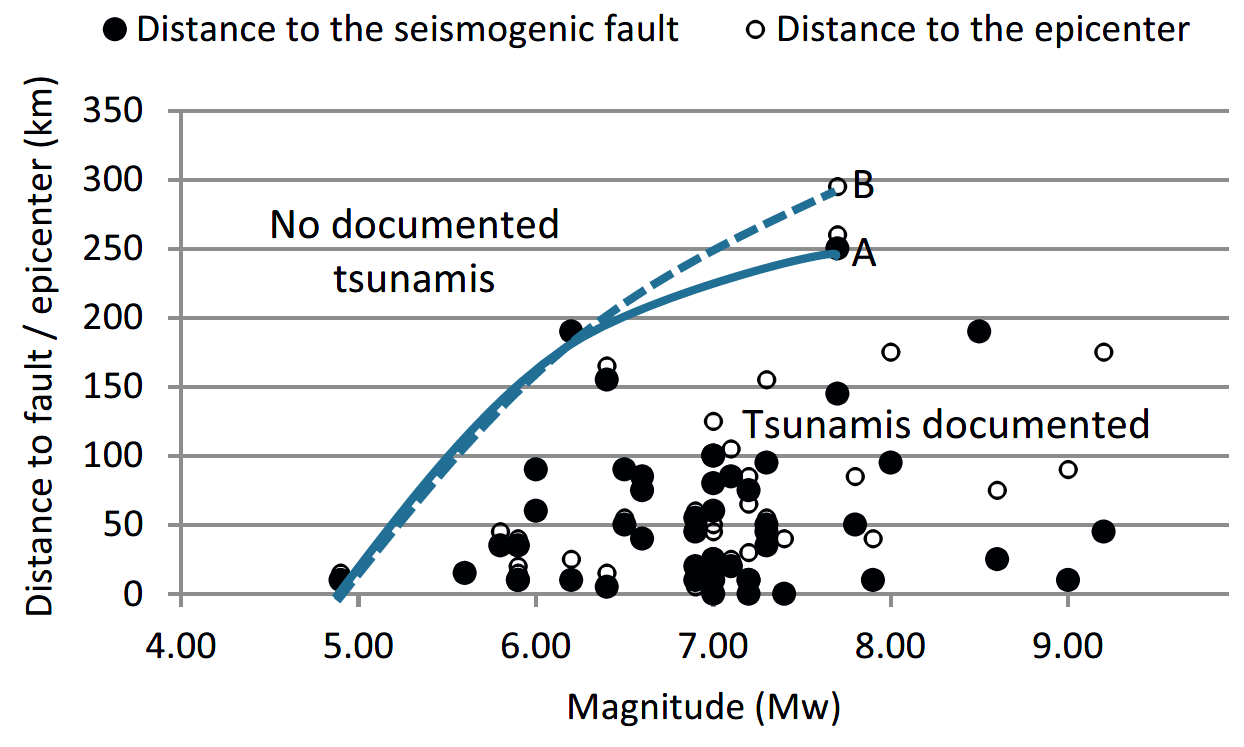
Fig. 4.

Empirical ‘Magnitude-Distance’ bounding envelopes for tsunamis generated by seismogenic submarine landslides. Filled circles denote the distance from the seismogenic fault to the landslide scar (R_f), and empty circles denote the distance between the earthquake epicenter and the landslide scar (R_e). The bounding envelope of the maximal distance between the seismogenic fault and the landslide scar is delineated by line A and the bounding envelope between the epicenter and the landslide scar is denoted by the dashed line B.

Salamon and Di Manna (2019)

References

Salamon, A., and Di Manna, P. (2019). "Empirical constraints on magnitude-distance relationships for seismically-induced submarine tsunamigenic landslides." Earth-Science Reviews 191: 66-92.

Explanation

This calculator estimates local seismic intensity from the thickness and deformation style of a seismite. Seismite type follows the classification scheme of Wetzler et al. (2010), which recognizes four principal deformation styles: linear waves, asymmetric billows, coherent vortices, and mixed or brecciated layers. Two independent intensity-estimation techniques are employed. The first is the Heifetz-Wetzler method, as presented in Lu et al. (2020), which relates seismite type and thickness to the ground shaking required to generate the observed deformation. The second is the Modified Williams method, which builds upon the approach developed in Williams (2004) while incorporating advances introduced by the Heifetz-Wetzler methodology. Because the two methods are based on different approaches, assumptions, and calibrations, the calculator reports both estimates as well as their arithmetic average. An optional site-effect correction based on Darvasi and Agnon (2019) may also be applied using V_S30 to account for local amplification or attenuation of ground motion caused by near-surface geological conditions.

Seismite Intensity Calculator

Variable	Input	Units	Notes
Seismite Thickness		cm	Thickness of deformed interval
Seismite Type		1-4	1 = linear waves; 2 = asymmetric billows; 3 = coherent vortices; 4 = breccia / mixed layer
V_S30		m/s	Used for site-effect adjustment (enter 655 for no site effect)
Variable	Output	Units	Notes
Bedrock Intensity		MMI	Heifetz-Wetzler technique as shown in Lu et al. (2020)
Bedrock Intensity		MMI	Modified Williams technique
Average Bedrock Intensity		MMI	Average of Heifetz-Wetzler and Modified Williams techniques
Bedrock Intensity		MMI	Heifetz-Wetzler technique as shown in Lu et al. (2020) with site effect using Vs30
Bedrock Intensity		MMI	Modified Williams technique with site effect using Vs30
Average Bedrock Intensity		MMI	Average of Heifetz-Wetzler and Modified Williams while considering site effect

References

Darvasi, Y. and Agnon, A. (2019). Calibrating a new attenuation curve for the Dead Sea region using surface-wave dispersion surveys in sites damaged by the 1927 Jericho earthquake. Solid Earth 10: 379-390.

Heifetz, E., Agnon, A., and Marco, S. (2005). Soft-sediment deformation by Kelvin-Helmholtz instability: A case from Dead Sea earthquakes. Earth and Planetary Science Letters 236: 497-504.

Lu, Y., Wetzler, N., Waldmann, N., Agnon, A., Biasi, G.P., and Marco, S. (2020). A 220,000-year-long continuous large earthquake record on a slow-slipping plate boundary. Science Advances 6(48): eaba4170.

Wetzler, N., Heifetz, E., and Marco, S. (2010). Quantitative Analysis of Seismogenic Shear-Induced Turbulence in Lake Sediments. Geophysical Journal International 181(1): 35-44.

Williams, J. (2004). Estimation of Earthquake Source Parameters from Soft Sediment Deformation Layers Present in Dead Sea Muds. M.S. Report, California State University - Long Beach

Explanation

Obermeier (1996) supplied a chart which can be used to estimate PGA (Peak Ground Acceleration) of earthquake induced Sand Boils.

Sand Boil Chart to estimate PGA

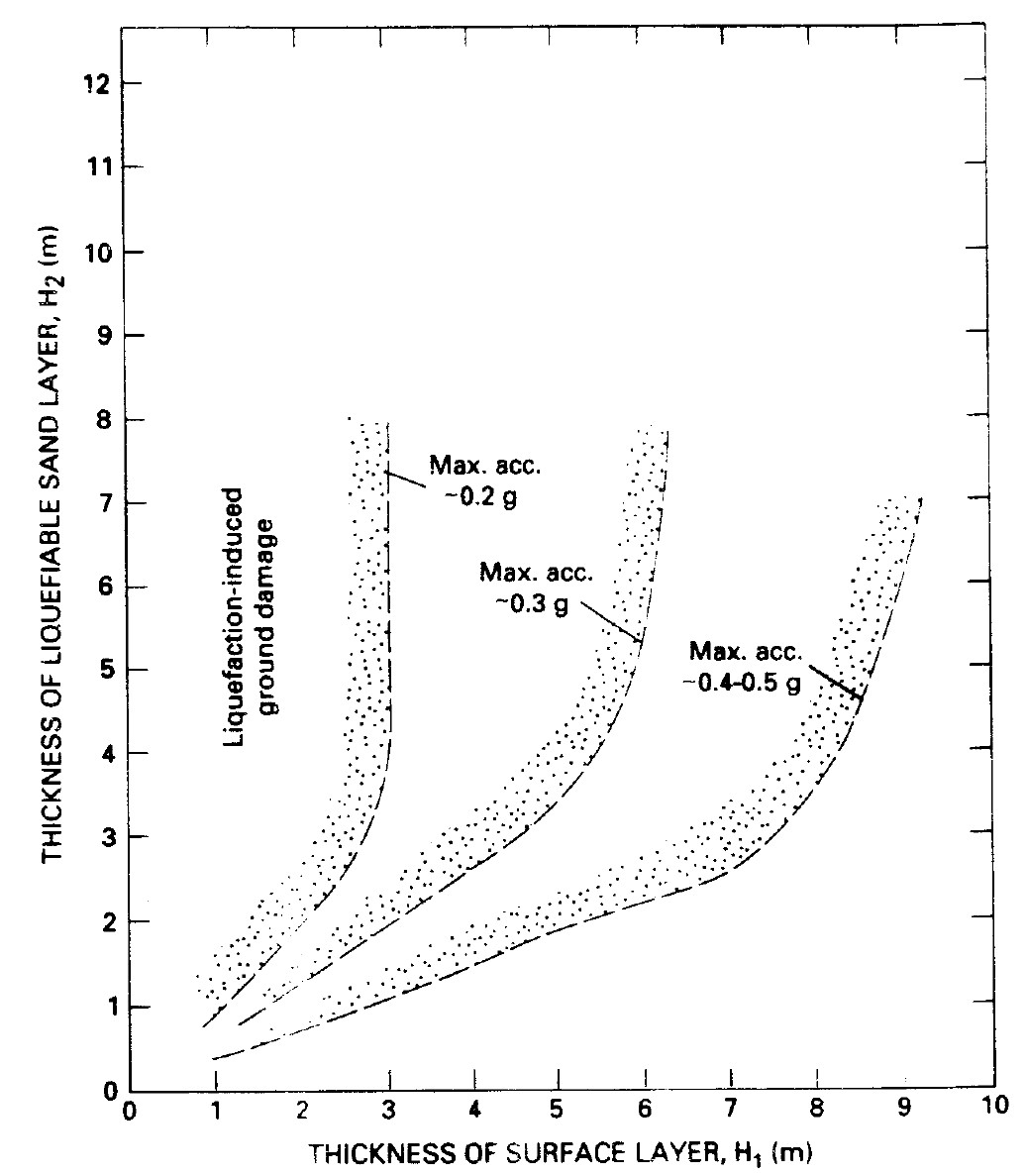
Fig. 9. - Proposed boundary curves relating thickness of nonliquefiable surface layer to thickness of the liquefiable zone as a function of peak earthquake accelerations required to induce venting or ground rupturing at the surface. From Ishihara (1985). Obermeier (1996)

Convert PGA to Intensity
Variable	Input	Units	Notes
PGA		g	Peak Horizontal Ground Acceleration
Variable	Output (No Site Effect)	Units	Notes
I		unitless	Conversion from PGA to Intensity using Wald et al (1999)

References

Ishihara, K. (1985). Stability of natural deposits during earthquakes. In: Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering. San Francisco, CA, USA, 1, 321-376.

Obermeier, S. F. (1996). "Use of liquefaction-induced features for paleoseismic analysis — An overview of how seismic liquefaction features can be distinguished from other features and how their regional distribution and properties of source sediment can be used to infer the location and strength of Holocene paleo-earthquakes." Engineering Geology 44(1-4): 1-76.

Rateria, G., and Maurer, B. W. (2022). "Evaluation and updating of Ishihara’s (1985) model for liquefaction surface expression, with insights from machine and deep learning." Soils and Foundations 62(3): 101131.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Calculators

Convert PGA to Intensity

Variable	Input	Units	Notes
PGA		g	Peak Horizontal Ground Acceleration
Variable	Output - Site Effect not considered	Units	Notes
I		unitless	Conversion from PGA to Intensity using Wald et al (1999)

Convert Surface Magnitude to Moment Magnitude

Source - Scordilis (2006) as shown in Darawcheh et al (2021)

Variable	Input	Units	Notes
M_S		unitless	Surface Magnitude
Variable	Output	Units	Notes
M_W		unitless	Moment Magnitude

References

Darawcheh, R., et al. (2021). "Empirical relationship for assessing the near-field horizontal coseismic displacement using GPS Seismology data." Geofísica Internacional 60: 31-50.

Scordilis, E. M. (2006). "Empirical global relations converting M_S and m_b to moment magnitude." Journal of Seismology 10(2): 225-236.

Wald, D. J., et al. (1999). "Relationships between Peak Ground Acceleration, Peak Ground Velocity, and Modified Mercalli Intensity in California." Earthquake Spectra 15(3): 557-564.

Online Calculators

Physics Calculators

SEISCALC

Earthquake Science Calculators

Coded by Jefferson Williams

Caveat: For use in Historical Earthquake Research - not for Engineering work.

Seismic Attenuation

Magnitude Estimation (Scaling Relationships)

SEISMERIO - The Paleoseismic Scenarios Explorer

V_S30 Site Effect

Slope Effect

Ridge Effect (aka Topographic Effect)

Radiation Patterns

Single-value calculator

Ratio vs period (fixed magnitude, several distances)

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Single-value calculator

Ratio vs period (fixed magnitude, several distances)

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Archaeoseismic Calculators

Tilt Method

PGV Estimation Method

Landslide Calculators

Static Analysis

Dynamic Analysis

Tsunami Calculators

Seismite Calculators

Sand Boils

Various Converters

Miscellaneous Calculators

SEISCALC

Earthquake Science Calculators

Coded by Jefferson Williams

Caveat: For use in Historical Earthquake Research - not for Engineering work.

Seismic Attenuation

Magnitude Estimation (Scaling Relationships)

SEISMERIO - The Paleoseismic Scenarios Explorer

VS30 Site Effect

Slope Effect

Ridge Effect (aka Topographic Effect)

Radiation Patterns

Single-value calculator

Ratio vs period (fixed magnitude, several distances)

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Single-value calculator

Ratio vs period (fixed magnitude, several distances)

Ratio vs distance (fixed period, the four magnitudes used by Somerville et al. 1997)

Archaeoseismic Calculators

Tilt Method

PGV Estimation Method

Landslide Calculators

Static Analysis

Dynamic Analysis

Tsunami Calculators

Seismite Calculators

Sand Boils

Various Converters

Miscellaneous Calculators

V_S30 Site Effect